题目内容
已知函数f(x)=sin2x+asinxcosx-cos2x,且
(1)求常数a的值及f(x)的最小值;
(2)当 时,求f(x)的单调增区间.
时,求f(x)的单调增区间.
解:(1)∵ ,
,
∴
∴a=2
∴f(x)=sin2x+2sinxcosx-cos2x=sin2x-cos2x=
当 ,k∈z,
,k∈z,
即 ,k∈z时
,k∈z时 取最小值-1,
取最小值-1,
从而f(x)取最小值 .(6分)
.(6分)
(2)令
即 ;k∈z
;k∈z
又 ,
,
∴f(x)在 上的单调递增(12分)
上的单调递增(12分)
分析:(1)由 ,把
,把 代入已知函数,可求a的值,把a代入到已知函数中,利用辅助角公式对函数化简可得
代入已知函数,可求a的值,把a代入到已知函数中,利用辅助角公式对函数化简可得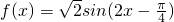 ,结合正弦函数的性质,当
,结合正弦函数的性质,当 ,k∈z,时
,k∈z,时 取最小值-1,从而可求函数的最小值
取最小值-1,从而可求函数的最小值
(2)令 结合
结合 ,可求
,可求
点评:本题主要考查了二倍角公式、辅助角公式的综合运用,把不同名的三角函数化简为一个角的三角函数,进而研究函数的性质.
 ,
,∴

∴a=2
∴f(x)=sin2x+2sinxcosx-cos2x=sin2x-cos2x=

当
 ,k∈z,
,k∈z,即
 ,k∈z时
,k∈z时 取最小值-1,
取最小值-1,从而f(x)取最小值
 .(6分)
.(6分)(2)令

即
 ;k∈z
;k∈z又
 ,
,∴f(x)在
 上的单调递增(12分)
上的单调递增(12分)分析:(1)由
 ,把
,把 代入已知函数,可求a的值,把a代入到已知函数中,利用辅助角公式对函数化简可得
代入已知函数,可求a的值,把a代入到已知函数中,利用辅助角公式对函数化简可得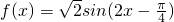 ,结合正弦函数的性质,当
,结合正弦函数的性质,当 ,k∈z,时
,k∈z,时 取最小值-1,从而可求函数的最小值
取最小值-1,从而可求函数的最小值(2)令
 结合
结合 ,可求
,可求点评:本题主要考查了二倍角公式、辅助角公式的综合运用,把不同名的三角函数化简为一个角的三角函数,进而研究函数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
