题目内容
已知向量 =(
=( sin2x-1,cosx),n=(
sin2x-1,cosx),n=( ,cosx),设函数f(x)=
,cosx),设函数f(x)= •
• .
.
(1)求函数f(x)的最小正周期及在[0, ]上的最大值;
]上的最大值;
(2)已知△ABC的角A、B、C所对的边分别为a、b、c,A、B为锐角,f(A+ )=
)= ,f(
,f( -
- )=
)= ,又a+b=
,又a+b= +1,求a、b、c的值.
+1,求a、b、c的值.
解:(1) ,(3分)
,(3分)
∴ ,
,
由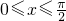 得
得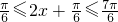 ,
,
∴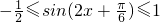 ,
,
∴f(x)max=1;(16分)
(2)∵ ,
,
∴ ,
,
∵A为锐角,∴ ,
, (7分)
(7分)
又 ,
,
∵B为锐角,∴ ,(8分)
,(8分)
由正弦定理知
又 ,b=1(10分)
,b=1(10分)
又∵sinC=sin(A+B)=sinA•cosB+cosA•sinB= ,
,
由 (12分)
(12分)
分析:(1)根据平面向量的数量积的运算法则即可得到f(x)的解析式,再利用二倍角的余弦函数公式及两角和的正弦函数公式化为一个角的正弦函数,利用周期公式即可求出f(x)的最小正周期,由x的范围求出这个角的范围,根据正弦函数的值域即可得到f(x)的值域,进而得到f(x)的最大值;
(2)由 ,代入f(x)并利用诱导公式化简后,即可得到cos2A的值,然后利用二倍角的余弦函数公式即可求出sinA的值,由A为锐角,利用同角三角函数间的基本关系即可求出cosA的值,又
,代入f(x)并利用诱导公式化简后,即可得到cos2A的值,然后利用二倍角的余弦函数公式即可求出sinA的值,由A为锐角,利用同角三角函数间的基本关系即可求出cosA的值,又 ,代入f(x)化简后即可求出sinB的值,由B的范围,利用同角三角函数间的基本关系即可求出cosB的值,由正弦定理,根据求出的sinA和sinB的值即可得到a与b的关系式,由a与b的和即可求出a与b的值,然后由sinA,cosA,sinB及cosB的值,根据诱导公式及两角和的正弦函数公式即可求出sinC的值,由b,sinB,sinC的值,利用正弦定理即可求出c的值.
,代入f(x)化简后即可求出sinB的值,由B的范围,利用同角三角函数间的基本关系即可求出cosB的值,由正弦定理,根据求出的sinA和sinB的值即可得到a与b的关系式,由a与b的和即可求出a与b的值,然后由sinA,cosA,sinB及cosB的值,根据诱导公式及两角和的正弦函数公式即可求出sinC的值,由b,sinB,sinC的值,利用正弦定理即可求出c的值.
点评:此题考查学生掌握平面向量的数量积的运算法则及正弦函数的值域,灵活运用两角和与差的正弦函数公式及正弦定理化简求值,灵活运用二倍角的余弦函数公式及同角三角函数间的基本关系化简求值,是一道中档题.
 ,(3分)
,(3分)∴
 ,
,由
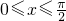 得
得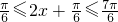 ,
,∴
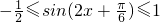 ,
,∴f(x)max=1;(16分)
(2)∵
 ,
,∴
 ,
,∵A为锐角,∴
 ,
, (7分)
(7分)又
 ,
,∵B为锐角,∴
 ,(8分)
,(8分)由正弦定理知

又
 ,b=1(10分)
,b=1(10分)又∵sinC=sin(A+B)=sinA•cosB+cosA•sinB=
 ,
,由
 (12分)
(12分)分析:(1)根据平面向量的数量积的运算法则即可得到f(x)的解析式,再利用二倍角的余弦函数公式及两角和的正弦函数公式化为一个角的正弦函数,利用周期公式即可求出f(x)的最小正周期,由x的范围求出这个角的范围,根据正弦函数的值域即可得到f(x)的值域,进而得到f(x)的最大值;
(2)由
 ,代入f(x)并利用诱导公式化简后,即可得到cos2A的值,然后利用二倍角的余弦函数公式即可求出sinA的值,由A为锐角,利用同角三角函数间的基本关系即可求出cosA的值,又
,代入f(x)并利用诱导公式化简后,即可得到cos2A的值,然后利用二倍角的余弦函数公式即可求出sinA的值,由A为锐角,利用同角三角函数间的基本关系即可求出cosA的值,又 ,代入f(x)化简后即可求出sinB的值,由B的范围,利用同角三角函数间的基本关系即可求出cosB的值,由正弦定理,根据求出的sinA和sinB的值即可得到a与b的关系式,由a与b的和即可求出a与b的值,然后由sinA,cosA,sinB及cosB的值,根据诱导公式及两角和的正弦函数公式即可求出sinC的值,由b,sinB,sinC的值,利用正弦定理即可求出c的值.
,代入f(x)化简后即可求出sinB的值,由B的范围,利用同角三角函数间的基本关系即可求出cosB的值,由正弦定理,根据求出的sinA和sinB的值即可得到a与b的关系式,由a与b的和即可求出a与b的值,然后由sinA,cosA,sinB及cosB的值,根据诱导公式及两角和的正弦函数公式即可求出sinC的值,由b,sinB,sinC的值,利用正弦定理即可求出c的值.点评:此题考查学生掌握平面向量的数量积的运算法则及正弦函数的值域,灵活运用两角和与差的正弦函数公式及正弦定理化简求值,灵活运用二倍角的余弦函数公式及同角三角函数间的基本关系化简求值,是一道中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目