题目内容
在△ABC中,三个内角之比为A:B:C=1:2:3,那么相对应的三边之比a:b:c等于
- A.
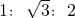
- B.1:2:3
- C.

- D.3:2:1
A
分析:根据三角形的内角和公式可得A=30°、B=60°、C=90°,再由正弦定理可得 a:b:c=sin30°:sin60°:
sin90°,运算求得结果.
解答:在△ABC中,三个内角之比为A:B:C=1:2:3,再由内角和公式可得A=30°,B=60°,
C=90°.再由正弦定理可得 a:b:c=sin30°:sin60°:sin90°=1: :2,
:2,
故选A.
点评:本题考查正弦定理,三角形的内角和公式,求出A=30°、B=60°、C=90°,是解题的关键.
分析:根据三角形的内角和公式可得A=30°、B=60°、C=90°,再由正弦定理可得 a:b:c=sin30°:sin60°:
sin90°,运算求得结果.
解答:在△ABC中,三个内角之比为A:B:C=1:2:3,再由内角和公式可得A=30°,B=60°,
C=90°.再由正弦定理可得 a:b:c=sin30°:sin60°:sin90°=1:
 :2,
:2,故选A.
点评:本题考查正弦定理,三角形的内角和公式,求出A=30°、B=60°、C=90°,是解题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目