题目内容
已知函数f(x)= .
.
(I)求证:不论a为何实数f(x)总为增函数;
(II)确定a的值,使f(x)为奇函数;
(Ⅲ)当f(x)为奇函数时,求f(x)的值域.
(I)证明:f(x)= =a-
=a- ,
,
设x1<x2,则f(x1)-f(x2)=(a- )-(a-
)-(a- )=
)=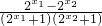 ,
,
因为x10,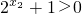 ,
,
所以f(x1)<-f(x2)<0,即f(x1)<f(x2).
故不论a为何实数f(x)总是为增函数;
(II)若f(x)为奇函数,则f(-x)=-f(x),即a- =-(a-
=-(a- ),
),
所以2a= +
+ =1,即a=
=1,即a= .
.
故当a= 时,f(x)为奇函数.
时,f(x)为奇函数.
(Ⅲ)由(II)知,若f(x)为奇函数,a= ,f(x)=
,f(x)= -
- ,
,
因为2x>0,所以0< <1,-1<-
<1,-1<- <0,所以-
<0,所以- <f(x)<
<f(x)< .
.
故f(x)的值域为(- ,
, ).
).
分析:(I)应用增函数的定义证明;
(II)根据奇函数定义,在定义域内f(-x)=-f(x)恒成立可求a值;
(Ⅲ)利用2x>0及函数单调性可求.
点评:本题考查函数的奇偶性、单调性,其定义是解决该类问题的基本方法.
 =a-
=a- ,
,设x1<x2,则f(x1)-f(x2)=(a-
 )-(a-
)-(a- )=
)=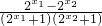 ,
,因为x10,
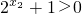 ,
,所以f(x1)<-f(x2)<0,即f(x1)<f(x2).
故不论a为何实数f(x)总是为增函数;
(II)若f(x)为奇函数,则f(-x)=-f(x),即a-
 =-(a-
=-(a- ),
),所以2a=
 +
+ =1,即a=
=1,即a= .
.故当a=
 时,f(x)为奇函数.
时,f(x)为奇函数.(Ⅲ)由(II)知,若f(x)为奇函数,a=
 ,f(x)=
,f(x)= -
- ,
,因为2x>0,所以0<
 <1,-1<-
<1,-1<- <0,所以-
<0,所以- <f(x)<
<f(x)< .
.故f(x)的值域为(-
 ,
, ).
).分析:(I)应用增函数的定义证明;
(II)根据奇函数定义,在定义域内f(-x)=-f(x)恒成立可求a值;
(Ⅲ)利用2x>0及函数单调性可求.
点评:本题考查函数的奇偶性、单调性,其定义是解决该类问题的基本方法.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|