题目内容
如图所示,四棱锥P—ABCD中,AB⊥AD,CD⊥AD,PA⊥面ABCD,PA=AD=CD=2AB.M为PC的中点,求: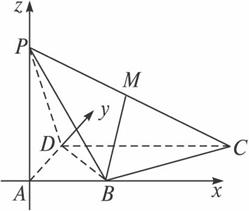
(1)BM与AD成的角;
(2)BM与平面PBD所成的角的正弦值;
(3)C点到面PBD的距离;
(4)二面角CBDP的余弦值.
答案:解法一:以A点为原点建立空间直角坐标系(如下图所示),

则B(1,0,0)、C(2,2,0)、D(0,2,0)、P(0,0,2)、M(1,1,1).
(1)∵cos〈![]() 〉=
〉=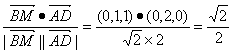 ,故BM与AD所成的角为45°.
,故BM与AD所成的角为45°.
(2)设平面PBD的法向量为n=(x,y,z),则n·![]() =(x,y,z)·(-1,2,0)=-x+2y=0,
=(x,y,z)·(-1,2,0)=-x+2y=0,
∴x=2y.
n·![]() =(x,y,z)·(0,2,-2)=2y-2z=0,
=(x,y,z)·(0,2,-2)=2y-2z=0,
∴z=y.
取y=1,则n=(2,1,1),∴cos(![]() ,n)=
,n)=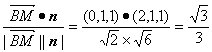 .
.
设BM与平面PBD所成的角为θ,则sinθ=cos(![]() ,n)=
,n)=![]() .即为所求.
.即为所求.
(3)C点到平面PBD的距离d=![]() .
.
(4)由于平面PBD的法向量n=(2,1,1),平面BCD的法向量为![]() =(0,0,2),
=(0,0,2),
而cos(![]() ·n)=
·n)=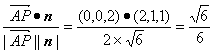 .
.
显然二面角CBDP的平面角为钝角,故所求的余弦值为![]() .
.
解法二:(1)取PD的中点N,连结MN,则MN∥DC且MN=2DC,∴MN∥AB且MN=AB,
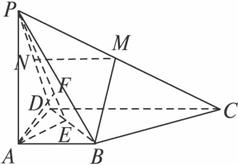
∴四边形ABMN为平行四边形,∴BM∥AN,∴∠NAD为异面直线BM与AD所成的角,
而PA⊥平面ABCD,∴PA⊥AD,且PA=AD,∴∠NAD=45°,故BM与AD所成的角为45°.(2)∵BM∥AN,∴BM与平面PBD所成角等于AN与平面PBD所成角.过A作AE⊥BD于E,连结PE,过A作AF⊥PE于F,
∵PA⊥平面ABCD,∴PA⊥BD,∴BD⊥平面PAE,∴AF⊥BD,
∴AF⊥平面PBD.∠ANF是AN与面PBD所成的角,在△ABD中,AD=2,AB=1,AB⊥AD,∴BD=![]() ,
,
∴AE=![]() .在△PAE中,PA=2,AE=
.在△PAE中,PA=2,AE=![]() ,PA⊥AE,∴PE=
,PA⊥AE,∴PE=![]() ,
,
∴AF=![]() .在△PAD中,PA=AD=2,PA⊥AD,∴AN=
.在△PAD中,PA=AD=2,PA⊥AD,∴AN=![]() ,
,
∴sin∠ANF=![]() .故BM与平面PBD所成角的正弦值为
.故BM与平面PBD所成角的正弦值为![]() .
.
(3)设C点到平面PBD的距离为d,
∵VC—PBD=VC—BCD,
∴![]() ×(
×(![]() ×BD×PE)×d=
×BD×PE)×d=![]() ×(
×(![]() ×CD×AD)×PA,∴d=
×CD×AD)×PA,∴d=![]() .
.
故C点到平面PBD的距离为![]() .
.
(4)由(2)知,BD⊥平面PAE,∴∠PEA为二面角ABDP的平面角.
又PE=![]() ,AE=
,AE=![]() ,
,
∴cos∠PEA=![]() .
.
而二面角ABDP与二面角CBDP互补,故二面角CBDP的余弦值为![]() .
.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点. 如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4, 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD. (2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.
(2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点. 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.