题目内容
将甲、乙、丙等六位同学排成一排,且甲、乙在丙的两侧,则不同的排法种数共有( )
A. | B. | C. | D. |
D
解析试题分析:本题属于排列组合中的定序问题,因此将甲、乙、丙等六位同学排成一排,且甲、乙在丙的两侧,则不同的排法种数共有2 =240种.
=240种.
考点:排列、组合及简单计数问题.

练习册系列答案
相关题目
设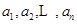 是
是 的一个全排列,把排在
的一个全排列,把排在 左边且小于
左边且小于 的数的个数称为
的数的个数称为 的顺序数(
的顺序数( ),例如在排列6,4,5,3,2,1中,5的顺序数是1而3的顺序数是0.在
),例如在排列6,4,5,3,2,1中,5的顺序数是1而3的顺序数是0.在 的全排列中,8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列的种数是( )
的全排列中,8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列的种数是( )
| A.48 | B.96 | C.144 | D.192 |
设已知 均为整数(
均为整数( ),若
),若 和
和 被
被 除所得的余数相同,则称
除所得的余数相同,则称 和
和 对模
对模 同余,记为
同余,记为  ,若
,若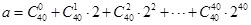 ,且
,且 , 则
, 则 的值可以是( )
的值可以是( )
| A.2011 | B.2012 | C.2013 | D.2014 |
甲、乙两人从4门课程中各选修1门,则甲、乙所选的课程不相同的选法共有 ( )
| A.6种 | B.12种 | C.30种 | D.36种 |
在高校自主招生中,某学校获得5个推荐名额,其中清华大学2名,北京大学2名,复旦大学1名。并且北京大学和清华大学都要求必须有男生参加。学校通过选拔定下3男2女共5个推荐对象,则不同的推荐方法共有( )
| A.20种 | B.22种 | C.24种 | D.36种 |
体育场南侧有4个大门,北侧有3个大门,某人到该体育场晨练,则他进出门的方案有( )
| A.12种 | B.7种 | C.24种 | D.49种 |
 (
( R)展开式中的常数项是( )
R)展开式中的常数项是( )
A. | B. | C.15 | D.20 |
6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品,已知6位同学之间共进行了13次交换,则收到 份纪念品的同学人数为( )
份纪念品的同学人数为( )
| A.1或3 |
| B.1或4 |
| C.2或3 |
| D.2或4 |
已知(x-m)7=a0+a1x+a2x2+…+a7x7的展开式中x5的系数是189,则实数m=( )
| A.3 | B.-3 | C.±3 | D.5 |