题目内容
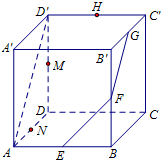 (2012•海淀区二模)在正方体ABCD-A'B'C'D'中,棱AB,BB',B'C',C'D'的中点分别是E,F,G,H,如图所示.
(2012•海淀区二模)在正方体ABCD-A'B'C'D'中,棱AB,BB',B'C',C'D'的中点分别是E,F,G,H,如图所示.(Ⅰ)求证:AD'∥平面EFG;
(Ⅱ)求证:A'C⊥平面EFG;
(Ⅲ)判断点A,D',H,F是否共面?并说明理由.
分析:(Ⅰ)利用正方体的性质以及题中的条件,证明FG∥AD',再根据直线和平面平行的判定定理证得AD'∥平面EFG.
(Ⅱ)利用直线和平面垂直的判定定理、性质定理证明BC'⊥A'C,A'C⊥EF,从而证明A'C⊥平面EFG.
(Ⅲ)点A,D',H,F不共面,用反证法证明如下:假设A,D',H,F共面,由(Ⅰ)可证得C'F∥BC',而C'F与BC'相交,这是矛盾的,故假设不对.
(Ⅱ)利用直线和平面垂直的判定定理、性质定理证明BC'⊥A'C,A'C⊥EF,从而证明A'C⊥平面EFG.
(Ⅲ)点A,D',H,F不共面,用反证法证明如下:假设A,D',H,F共面,由(Ⅰ)可证得C'F∥BC',而C'F与BC'相交,这是矛盾的,故假设不对.
解答: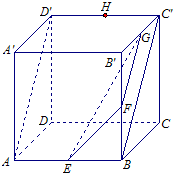 (Ⅰ)证明:连接BC',在正方体ABCD-A'B'C'D'中,AB=C'D',AB∥C'D'.
(Ⅰ)证明:连接BC',在正方体ABCD-A'B'C'D'中,AB=C'D',AB∥C'D'.
所以,四边形ABC'D'是平行四边形,所以,AD'∥BC'.
因为 F,G分别是BB',B'C'的中点,所以 FG∥BC',所以,FG∥AD'.
因为 EF,AD'是异面直线,所以,AD'?平面EFG.
因为 FG?平面EFG,所以,AD'∥平面EFG.
(Ⅱ)证明:连接B'C,在正方体ABCD-A'B'C'D'中,A'B'⊥平面BCC'B',BC'?平面BCC'B',所以,A'B'⊥BC'.
在正方形BCC'B'中,B'C⊥BC',
因为 A'B'?平面A'B'C,B'C?平面A'B'C,A'B'∩B'C=B',所以,BC'⊥平面A'B'C.
因为 A'C?平面A'B'C,所以,BC'⊥A'C.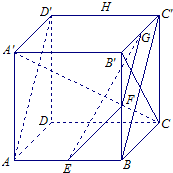
因为 FG∥BC',所以,A'C⊥FG,同理可证:A'C⊥EF.
因为 EF?平面EFG,FG?平面EFG,EF∩FG=F,所以,A'C⊥平面EFG.
(Ⅲ)点A,D',H,F不共面.理由如下:
假设A,D',H,F共面.连接C'F,AF,HF.
由(Ⅰ)知,AD'∥BC',因为 BC'?平面BCC'B',AD'?平面BCC'B',所以,AD'∥平面BCC'B'.
因为 C'∈D'H,所以,平面AD'HF∩平面BCC'B'=C'F.
因为 AD'?平面AD'HF,所以 AD'∥C'F.
所以,C'F∥BC',而C'F与BC'相交,矛盾.
所以,点A,D',H,F不共面.
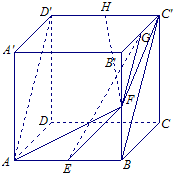
 (Ⅰ)证明:连接BC',在正方体ABCD-A'B'C'D'中,AB=C'D',AB∥C'D'.
(Ⅰ)证明:连接BC',在正方体ABCD-A'B'C'D'中,AB=C'D',AB∥C'D'.所以,四边形ABC'D'是平行四边形,所以,AD'∥BC'.
因为 F,G分别是BB',B'C'的中点,所以 FG∥BC',所以,FG∥AD'.
因为 EF,AD'是异面直线,所以,AD'?平面EFG.
因为 FG?平面EFG,所以,AD'∥平面EFG.
(Ⅱ)证明:连接B'C,在正方体ABCD-A'B'C'D'中,A'B'⊥平面BCC'B',BC'?平面BCC'B',所以,A'B'⊥BC'.
在正方形BCC'B'中,B'C⊥BC',
因为 A'B'?平面A'B'C,B'C?平面A'B'C,A'B'∩B'C=B',所以,BC'⊥平面A'B'C.
因为 A'C?平面A'B'C,所以,BC'⊥A'C.

因为 FG∥BC',所以,A'C⊥FG,同理可证:A'C⊥EF.
因为 EF?平面EFG,FG?平面EFG,EF∩FG=F,所以,A'C⊥平面EFG.
(Ⅲ)点A,D',H,F不共面.理由如下:
假设A,D',H,F共面.连接C'F,AF,HF.
由(Ⅰ)知,AD'∥BC',因为 BC'?平面BCC'B',AD'?平面BCC'B',所以,AD'∥平面BCC'B'.
因为 C'∈D'H,所以,平面AD'HF∩平面BCC'B'=C'F.
因为 AD'?平面AD'HF,所以 AD'∥C'F.
所以,C'F∥BC',而C'F与BC'相交,矛盾.
所以,点A,D',H,F不共面.

点评:本题主要考查直线和平面平行的判定定理、性质定理的应用;直线和平面垂直的判定定理、性质定理的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目