题目内容
| |||||||||||||||
解析:
(1) |
证明:连结BD交AC于点O,连结EO.
∴EO//PB.……………………1分
∴PB//平面AEC.……………………3分 |
(2) |
证明: ∴PA⊥平面ABCD.
∴ 又 ∴CD 又 ∴平面 |
(3) |
解法一:过点B作BH 易证 ∴
∴AB为斜线PB在平面ABCD内的射影, 又BC⊥AB, ∴BC⊥PB. 又BH ∴
在
= ∴ ∴二面角B—PC—D的大小为 解法二:如图,以A为坐标原点, 为
由PA=AB=2可知A、B、C、D、P的坐标分别为 A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2).
设平面BCP的法向量为 则 ∴ 令 设平面DCP的法向量为 则 ∴ 令
∴二面角B—PC—D的大小为 |

 阅读快车系列答案
阅读快车系列答案



 ,……………………12分
,……………………12分
 即
即

 即
即

 ,
,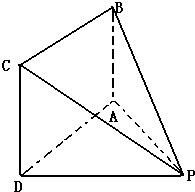 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,且
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,且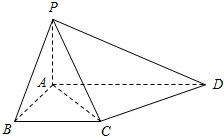 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=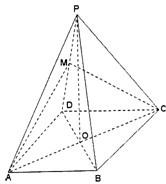 如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AB∥CD,AD=BC=2,对角线AC⊥BD于O,∠DAO=60°,且PO⊥平面ABCD,直线PA与底面ABCD所成的角为60°,M为PD上的一点.
如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AB∥CD,AD=BC=2,对角线AC⊥BD于O,∠DAO=60°,且PO⊥平面ABCD,直线PA与底面ABCD所成的角为60°,M为PD上的一点. 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F. 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.