题目内容
 直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=1,AA1=2,D是B1C1的中点,求点C与平面A1BD的距离.
直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=1,AA1=2,D是B1C1的中点,求点C与平面A1BD的距离.
解:法一:以C为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,
设平面A1BD的一个法向量
则
求出平面A1BD的一个法向量
然后用点到平面的距离公式 (6)
(6)
法二:也可用等体积原理计算出:
 ,
,


∴点C与平面A1BD的距离: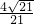 .
.
分析:法一:先建立空间直角坐标系,求出相关向量,利用向量垂直时数量积等于0求得法向量,结合点点C与平面A1BD的距离即可求解.
法二:也可用等体积原理计算,即视点C与平面A1BD的距离为三棱锥的高,结合等体积: 求得点C与平面A1BD的距离.
求得点C与平面A1BD的距离.
点评:本题考查点、线、面间的距离计算,正确分析题目的条件,找出几何体中的直线与平面之间的关系,即可获得解题思路.利用图形建立适当的空间直角坐标系是本题的关键.
设平面A1BD的一个法向量

则

求出平面A1BD的一个法向量

然后用点到平面的距离公式
 (6)
(6)法二:也可用等体积原理计算出:
 ,
,


∴点C与平面A1BD的距离:
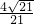 .
.分析:法一:先建立空间直角坐标系,求出相关向量,利用向量垂直时数量积等于0求得法向量,结合点点C与平面A1BD的距离即可求解.
法二:也可用等体积原理计算,即视点C与平面A1BD的距离为三棱锥的高,结合等体积:
 求得点C与平面A1BD的距离.
求得点C与平面A1BD的距离.点评:本题考查点、线、面间的距离计算,正确分析题目的条件,找出几何体中的直线与平面之间的关系,即可获得解题思路.利用图形建立适当的空间直角坐标系是本题的关键.

练习册系列答案
相关题目
 直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,AB1=
直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,AB1= 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直线B1C与平面ABC成30°角.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直线B1C与平面ABC成30°角. 如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是( )
如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是( ) 如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是
如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是







