题目内容
设f(x)=1+x+(1+x)2+…+(1+x)n(x≠0,n∈N*)的展开式中x项的系数为Tn,则
( )
| lim |
| x→∞ |
| Tn |
| n2+n |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
分析:首先找出f(x)展开式中x项的系数Tn的通项公式,代入极限中求出即可.
解答:解:因为第一项x的系数为0;前两项系数和为0+1=1;前三项系数和为0+1+2=3;…;
前n项的系数和为Tn=0+1+2+3+…+n-1=
;
=
=
=
故选A
前n项的系数和为Tn=0+1+2+3+…+n-1=
| (n-1)n |
| 2 |
| lim |
| n→∞ |
| Tn |
| n2+n |
| lim |
| n→∞ |
| ||
| n2+n |
| lim |
| n→∞ |
| ||||
1+
|
| 1 |
| 2 |
故选A
点评:考查学生利用二项式定理找x系数的能力,以及求极限及运算的能力.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
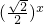 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是 ,1)
,1)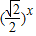 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( ) ,1)
,1)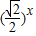 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( ) ,1)
,1)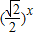 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( ) ,1)
,1)