题目内容
已知函数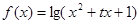 (
(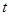 为常数,且
为常数,且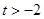 ).
).
(1)当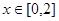 时,求函数
时,求函数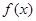 的最小值(用
的最小值(用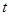 表示);
表示);
(2)是否存在不同的实数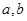 使得
使得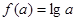 ,
,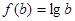 ,并且
,并且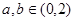 ,若存在,求出实数
,若存在,求出实数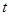 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
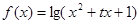 (
(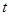 为常数,且
为常数,且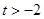 ).
).(1)当
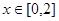 时,求函数
时,求函数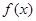 的最小值(用
的最小值(用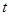 表示);
表示);(2)是否存在不同的实数
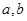 使得
使得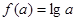 ,
,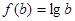 ,并且
,并且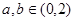 ,若存在,求出实数
,若存在,求出实数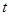 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.(1)函数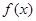 的最小值为
的最小值为 ;
;
(2)满足条件的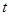 存在,取值范围为
存在,取值范围为 .
.
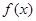 的最小值为
的最小值为 ;
;(2)满足条件的
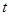 存在,取值范围为
存在,取值范围为 .
.试题分析:(1)构造新函数
 ,分
,分 和
和 两种情况讨论即可;(2)假设存在,则由已知得
两种情况讨论即可;(2)假设存在,则由已知得  ,等价于
,等价于 在区间
在区间 上有两个不同的实根,作出函数图象,可得
上有两个不同的实根,作出函数图象,可得 .
. 
试题解析:(1)令
 1分
1分当
 即
即 时,
时,  4分
4分当
 即
即 时,
时, 7分
7分综上:
 . 8分
. 8分(2)解法一:假设存在,则由已知得
 ,等价于
,等价于 在区间
在区间 上有两个不同的实根 11分
上有两个不同的实根 11分令
 ,则
,则 在
在 上有两个不同的零点
上有两个不同的零点 . 15分
. 15分解法2:假设存在,则由已知得

等价于
 在区间
在区间 上有两个不同的实根 11分
上有两个不同的实根 11分等价于
 ,作出函数图象,可得
,作出函数图象,可得 . 15分
. 15分
练习册系列答案
相关题目
 .
. -4
-4 +2的最大值和最小值.
+2的最大值和最小值. 在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上是( )
在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上是( )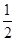 ≤t≤
≤t≤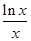
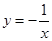 在
在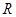 上单调递增;
上单调递增;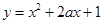 在
在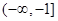 上单调递减,则
上单调递减,则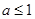 ;
;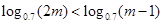 ,则
,则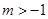 ;
;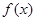 是定义在
是定义在 .
.