题目内容
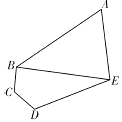
【题目】某学校的平面示意图为如下图五边形区域ABCDE，其中三角形区域ABE为生活区，四边形区域BCDE为教学区，AB，BC，CD，DE，EA，BE为学校的主要道路（不考虑宽度）. 
， 
． 
（1）求道路BE的长度；
（2）求生活区△ABE面积的最大值．
【答案】
（1）解：
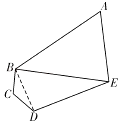
如图，连接BD，在△BCD中，由余弦定理得： 
，
∴ 
．
∵BC=CD，∴ 
，
又 
，∴ 
．
在Rt△BDE中，所以 
（2）解：设∠ABE=α，∵ 
，∴ 
．
在△ABE中，由正弦定理，得 
，
∴ 
．
∴ 
= 
．
∵ 
，∴ 
．
∴当 
，即 
时，S△ABE取得最大值为 
，
即生活区△ABE面积的最大值为 
注：第（2）问也可用余弦定理和均值不等式求解
【解析】（1）连接BD，在△BCD中，由余弦定理得：BD，在Rt△BDE中，求解BE即可．（2）设∠ABE=α，在△ABE中，由正弦定理，求解AB，AE，表示S△ABE ， 然后求解最大值．
练习册系列答案
相关题目
【题目】某市为了缓解城市交通压力，大力发展公共交通，提倡多坐公交少开车，为了调查市民乘公交车的候车情况，交通主管部门从在某站台等车的
名候车乘客中随机抽取
人，按照他们的候车时间（单位：分钟）作为样本分成
组，如下表所示：
组别 | 一 | 二 | 三 | 四 | 五 | 六 |
候车时间 |
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
（1）估计这名乘客中候车时间少于
分钟的人数；
（2）若从上表第四、五组的
人中随机抽取
人做进一步的问卷调查，求抽到的人恰好来自不同组的概率．
