题目内容
 如图组合体由直三棱柱ABC-A1B1C1与正三棱锥B-ACD组成,其中,AB⊥BC.它的正视图、俯视图、从左向右的侧视图的面积分别为2
如图组合体由直三棱柱ABC-A1B1C1与正三棱锥B-ACD组成,其中,AB⊥BC.它的正视图、俯视图、从左向右的侧视图的面积分别为2| 2 |
| 2 |
(Ⅰ)求直线CA1与平面ACD所成角的正弦;
(Ⅱ)在线段AC1上是否存在点P,使B1P⊥平面ACD.若存在,确定点P的位置;若不存在,说明理由.
分析:(Ⅰ) 根据正视图、俯视图、从左向右的侧视图的面积分别为2
+1,2
+1,1,从而可确定BA,BB1的长.以点B为原点,分别以BC、BB1、BA为x轴、y轴、z轴建立空间直角坐标系,求出平面ACD的法向量,进而可利用夹角公式求出直线CA1与平面ACD所成角的正弦;
(Ⅱ)假设存在
=m
=(
m,2m,-
m),利用
与平面ACD的法向量,得方程即可求解.
| 2 |
| 2 |
(Ⅱ)假设存在
| AP |
| AC1 |
| 2 |
| 2 |
| B1P |
解答:解:(1)设BA=BC=BD=a,BB1=b
由条件
⇒
.(3分)
以点B为原点,分别以BC、BB1、BA为x轴、y轴、z轴建立空间直角坐标系,则
A(0,0,
),C(
,0,0),D(0,-
,0),B1(0,2,0),C1(
,2,0),A1(0,2,
)(5分)
∵△ACD的重心G(
,-
,
)∴
=
=(
,-
,
)为平面ACD的法向量.(7分)
又
=(-
,2,
),则cos?
,
>=
=
(9分)
∴所求角的正弦值为
.(10分)
(2)令
=m
=(
m,2m,-
m)(11分)
=
+
=(
m,2m-2,
-
m)=λ
∴
∴无解(14分)
∴不存在满足条件的点P.
由条件
|
|
以点B为原点,分别以BC、BB1、BA为x轴、y轴、z轴建立空间直角坐标系,则
A(0,0,
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
∵△ACD的重心G(
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| a |
| BG |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
又
| CA1 |
| 2 |
| 2 |
| a |
| CA1 |
-
| ||||||
2
|
| ||
| 6 |
∴所求角的正弦值为
| ||
| 6 |
(2)令
| AP |
| AC1 |
| 2 |
| 2 |
| B1P |
| B1A |
| AP |
| 2 |
| 2 |
| 2 |
| a |
∴
|
∴不存在满足条件的点P.
点评:本题以组合体为载体,考查线面角,考查线面存在,关键是构建空间直角坐标系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,放置在水平面上的组合体由直三棱柱ABC-A1B1C1与正三棱锥B-ACD组成,其中,AB⊥BC,AB=
如图所示,放置在水平面上的组合体由直三棱柱ABC-A1B1C1与正三棱锥B-ACD组成,其中,AB⊥BC,AB=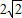 +1,
+1, +1,1.
+1,1.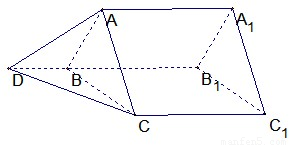
 ,BB1=2.
,BB1=2.