题目内容
△ABC的内角A、B、C的对边长分别为a、b、c,若a2-c2=b,且b=3ccosA,则b= .
【答案】分析:利用余弦定理将角化成边的等量关系,然后根据a2-c2=b消去a与c得到关于b的方程,解之即可.
解答:解:∵b=3ccosA
∴b=3c×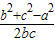 化简得2b2=3b2+3(c2-a2)
化简得2b2=3b2+3(c2-a2)
将a2-c2=b代入上式得2b2=3b2-3b
解得b=3
故答案为:3
点评:本题主要考查了余弦定理的应用,同时考查了运算求解的能力,属于中档题.
解答:解:∵b=3ccosA
∴b=3c×
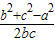 化简得2b2=3b2+3(c2-a2)
化简得2b2=3b2+3(c2-a2)将a2-c2=b代入上式得2b2=3b2-3b
解得b=3
故答案为:3
点评:本题主要考查了余弦定理的应用,同时考查了运算求解的能力,属于中档题.

练习册系列答案
相关题目