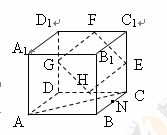
题目内容
四棱锥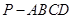 中,
中, ⊥底面
⊥底面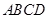 ,
,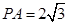 ,
, ,
,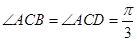 .
.

(Ⅰ)求证: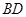 ⊥平面
⊥平面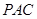 ;
;
(Ⅱ)若侧棱 上的点
上的点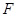 满足
满足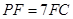 ,求三棱锥
,求三棱锥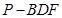 的体积.
的体积.
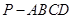 中,
中, ⊥底面
⊥底面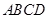 ,
,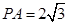 ,
, ,
,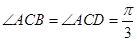 .
.
(Ⅰ)求证:
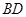 ⊥平面
⊥平面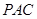 ;
;(Ⅱ)若侧棱
 上的点
上的点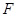 满足
满足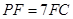 ,求三棱锥
,求三棱锥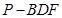 的体积.
的体积.(Ⅰ)见解析;(Ⅱ) .
.
 .
.试题分析:(Ⅰ)通过在平面PAC内证明PA和AC均与BD垂直,由线面垂直的判定定理得出结论;(Ⅱ)由割补法知
 ,故先求
,故先求 .处理的关键是利用图形分割.
.处理的关键是利用图形分割.试题解析:(Ⅰ)证明:因为BC=CD,即
 为等腰三角形,又
为等腰三角形,又 ,故
,故 .
.因为
 底面
底面 ,所以
,所以 ,从而
,从而 与平面
与平面 内两条相交直线
内两条相交直线 都垂直,
都垂直,故
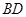 ⊥平面
⊥平面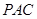 .
.(Ⅱ)解:
 .
.由
 底面
底面 知
知 .
. 由
 得三棱锥
得三棱锥 的高为
的高为 ,
,故:



练习册系列答案
相关题目
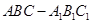 的底面是边长为
的底面是边长为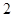 的正三角形,侧棱垂直于底面,侧棱长为
的正三角形,侧棱垂直于底面,侧棱长为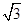 ,D为棱
,D为棱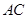 的中点。
的中点。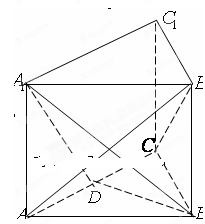
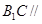 平面
平面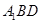 ;
;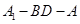 的大小.
的大小. ,?O的直径AB=2, C为弧AB的中点,D为AC的中点.
,?O的直径AB=2, C为弧AB的中点,D为AC的中点.
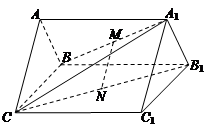
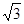 ,BC=2,求二面角A—A1C—B的余弦值的大小
,BC=2,求二面角A—A1C—B的余弦值的大小 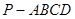 中,底面
中,底面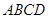 是矩形,
是矩形,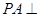 底面
底面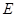 是
是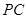 的中点,已知
的中点,已知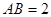 ,
,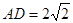 ,
,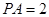 ,
,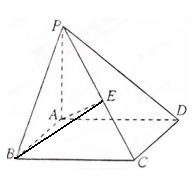
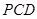 的面积;(II)三棱锥
的面积;(II)三棱锥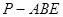 的体积
的体积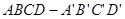 的外接球直径为
的外接球直径为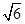 ,底面边长
,底面边长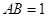 ,则侧棱
,则侧棱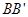 与平面
与平面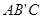 所成角的正切值为_________。
所成角的正切值为_________。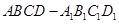 中,
中,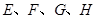 分别是
分别是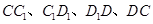 的中点,
的中点,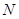 是
是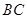 的中点,点
的中点,点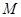 在四边形
在四边形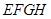 上或其内部运动,且使
上或其内部运动,且使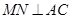 ,对于下列命题:①点
,对于下列命题:①点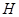 重合;②点
重合;②点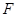 重合;③点
重合;③点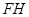 上;④点
上;④点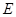 重合.
重合.