题目内容
设α,β是实系数方程x2+ax+2b=0的两个根,且α∈(0,1),β∈(1,2),则A.(![]() ,1) B.(
,1) B.(![]() ,1) C.(
,1) C.(![]() ) D.(
) D.(![]() )
)
答案:A 设f(x)=x2+ax+2b,由题意得 ,即
,即 ,在坐标平面内作出可行域,因为
,在坐标平面内作出可行域,因为![]() 表示过A(1,2)与P(a,b)直线的斜率,P在可行域内,因此
表示过A(1,2)与P(a,b)直线的斜率,P在可行域内,因此![]() ∈(
∈(![]() ),即
),即![]() ∈(
∈(![]() ,1),所以选A.
,1),所以选A.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 (其中
(其中 是虚数单位)是实系数方程
是虚数单位)是实系数方程 的一个根,求
的一个根,求 的值.
的值.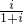 (其中i是虚数单位)是实系数方程2x2-mx+n=0的一个根,求|m+ni|的值.
(其中i是虚数单位)是实系数方程2x2-mx+n=0的一个根,求|m+ni|的值.