题目内容
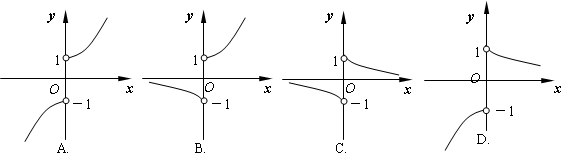
已知定义在R上的偶函数f(x)满足:?x∈R恒有f(x+2)=f(x)-f(1).且当x∈[2,3]时,f(x)=-2(x-3)2.若函数y=f(x)-loga(x+1)在(0,+∞)上至少有三个零点,则实数a的取值范围为( )
A.(0, ) ) | B.(0,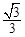 ) ) | C.(1,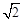 ) ) | D.(1,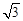 ) ) |
B
解析试题分析: 令x=-3,则f(-1)=f(-3)-f(1),因为f(x)是偶函数,所以f(1)=0,即f(x+2)=f(x),故函数f(x)是以2为周期的周期性函数,做出函数f(x)的图象,如图所示,要使y=f(x)-loga(x+1)在(0,+∞)上至少有三个零点,则 ,解得0<a<
,解得0<a<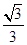 .
.
考点:1.周期函数;2.函数的零点;3.函数奇偶性的性质.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知函数 ,若
,若 ,则实数
,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
设奇函数f(x)在(0,+∞)上为单调递减函数,且f(2)=0,则不等式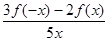 ≤0的解集为 ( )
≤0的解集为 ( )
| A.(-∞,-2]∪(0,2] | B.[-2,0]∪[2,+∞) |
| C.(-∞,-2]∪[2,+∞) | D.[-2,0)∪(0,2] |
函数 的定义域为( )
的定义域为( )
A. | B. | C. | D. |


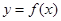 ,如果存在区间
,如果存在区间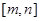 ,同时满足下列条件:①
,同时满足下列条件:① 在
在 存在“和谐区间”,则
存在“和谐区间”,则 的取值范围是( )
的取值范围是( )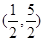
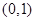
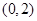
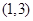
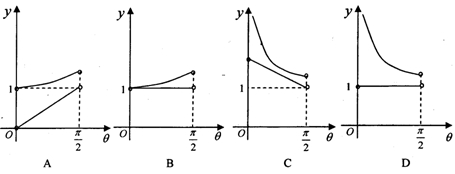
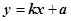 的图象如右图所示,则函数
的图象如右图所示,则函数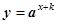 的可能图象是( )
的可能图象是( )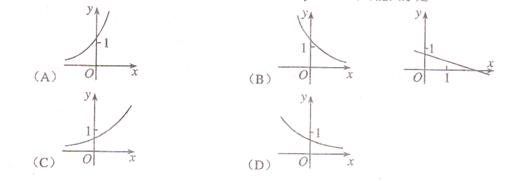
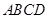 中,
中,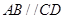 ,且
,且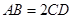 ,设
,设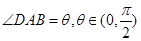 ,以
,以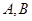 为焦点且过点
为焦点且过点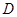 的双曲线的离心率为
的双曲线的离心率为 ,以
,以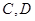 为焦点且过点
为焦点且过点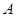 的椭圆的离心率为
的椭圆的离心率为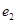 ,设
,设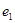 =
=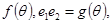 则
则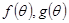 的大致图像是( )
的大致图像是( )
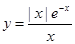 的图像的大致形状是( )
的图像的大致形状是( )