题目内容
设函数 的图象为C,给出下列命题:
的图象为C,给出下列命题:
①图象C关于直线 对称;
对称;
②函数f(x)在区间 内是增函数;
内是增函数;
③函数f(x)是奇函数;
④图象C关于点 对称.
对称.
⑤|f(x)|的周期为π
其中,正确命题的编号是________.(写出所有正确命题的编号)
①②
分析:①∵ =
= =-1,∴f(x)在
=-1,∴f(x)在 处取得最小值,可判断出其图象关于此直线对称;
处取得最小值,可判断出其图象关于此直线对称;
②由x∈ ,则
,则 ,从而
,从而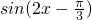 在区间
在区间 上单调递增,进而可判断f(x)的单调性;
上单调递增,进而可判断f(x)的单调性;
③判断f(-x)=-f(x)是否成立即可;
④判断 是否成立即可;
是否成立即可;
⑤判断 =|f(x)|,|f(x+π)|=|f(x)|是否成立即可.
=|f(x)|,|f(x+π)|=|f(x)|是否成立即可.
解答:①∵ =
= =-1,∴图象C关于直线
=-1,∴图象C关于直线 对称,正确;
对称,正确;
②若x∈ ,则
,则 ,∴
,∴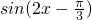 在区间
在区间 上单调递增,从而函数f(x)在区间
上单调递增,从而函数f(x)在区间 内是增函数,故正确;
内是增函数,故正确;
③f(-x)= =
= ≠
≠ ,∴函数f(x)不是奇函数,不正确;
,∴函数f(x)不是奇函数,不正确;
④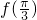 =
= =
= =
= ≠0,故图象C关于点
≠0,故图象C关于点 不对称,不正确;
不对称,不正确;
⑤∵ =
= =
= =
= =|f(x)|,而
=|f(x)|,而 ,因此|f(x)|的周期为
,因此|f(x)|的周期为 ,故不正确.
,故不正确.
综上可知:只有①②正确.
故答案为①②.
点评:熟练掌握三角函数的图象和性质是解题的关键.
分析:①∵
 =
= =-1,∴f(x)在
=-1,∴f(x)在 处取得最小值,可判断出其图象关于此直线对称;
处取得最小值,可判断出其图象关于此直线对称;②由x∈
 ,则
,则 ,从而
,从而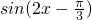 在区间
在区间 上单调递增,进而可判断f(x)的单调性;
上单调递增,进而可判断f(x)的单调性;③判断f(-x)=-f(x)是否成立即可;
④判断
 是否成立即可;
是否成立即可;⑤判断
 =|f(x)|,|f(x+π)|=|f(x)|是否成立即可.
=|f(x)|,|f(x+π)|=|f(x)|是否成立即可.解答:①∵
 =
= =-1,∴图象C关于直线
=-1,∴图象C关于直线 对称,正确;
对称,正确;②若x∈
 ,则
,则 ,∴
,∴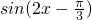 在区间
在区间 上单调递增,从而函数f(x)在区间
上单调递增,从而函数f(x)在区间 内是增函数,故正确;
内是增函数,故正确;③f(-x)=
 =
= ≠
≠ ,∴函数f(x)不是奇函数,不正确;
,∴函数f(x)不是奇函数,不正确;④
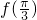 =
= =
= =
= ≠0,故图象C关于点
≠0,故图象C关于点 不对称,不正确;
不对称,不正确;⑤∵
 =
= =
= =
= =|f(x)|,而
=|f(x)|,而 ,因此|f(x)|的周期为
,因此|f(x)|的周期为 ,故不正确.
,故不正确.综上可知:只有①②正确.
故答案为①②.
点评:熟练掌握三角函数的图象和性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的图象为C,给出下列命题:
的图象为C,给出下列命题: 对称;
对称; 内是增函数;
内是增函数; 对称.
对称.