题目内容
【题目】已知函数 ![]() .
.
(1)判断并证明f(x)的奇偶性;
(2)求证: ![]() ;
;
(3)已知a,b∈(﹣1,1),且 ![]() ,
, ![]() ,求f(a),f(b)的值.
,求f(a),f(b)的值.
【答案】
(1)
解:由 ![]() 可得函数的定义域(﹣1,1),关于原点对称
可得函数的定义域(﹣1,1),关于原点对称
∵ ![]() =
= ![]() 故函数f(x)为奇函数
故函数f(x)为奇函数
(2)
解:∵f(a)+f(b)= ![]() =
= ![]()
![]() =
= 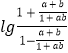 =
= ![]()
∴ ![]()
(3)
解:∵ ![]() =1
=1
∴f(a)+f(b)=1 ![]() =2
=2
∴f(a)+f(﹣b)=2
∵f(﹣b)=﹣f(b),
∴f(a)﹣f(b)=2,解得: ![]()
【解析】(1)由 ![]() 可得函数的定义域(﹣1,1),关于原点对称,再由
可得函数的定义域(﹣1,1),关于原点对称,再由 ![]() =
= ![]() 可判断函数奇偶性(2)分别计算 f(a)+f(b)与
可判断函数奇偶性(2)分别计算 f(a)+f(b)与 ![]() 可证(3)由(2)
可证(3)由(2) ![]() 可得f(a)+f(b)=1
可得f(a)+f(b)=1 ![]() ,f(a)+f(b)=2结合奇函数的性质可得f(﹣b)=﹣f(b),从而可求
,f(a)+f(b)=2结合奇函数的性质可得f(﹣b)=﹣f(b),从而可求
【考点精析】根据题目的已知条件,利用函数奇偶性的性质的相关知识可以得到问题的答案,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.

练习册系列答案
相关题目