题目内容
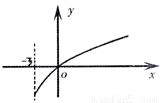已知函数f（x）的定义域为[-3，+∞），且f（6）=f（-3）=2．f′（x）为f（x）的导函数，f′（x）的图象如图所示．若正数a，b满足f（2a+b）＜2，则
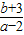的取值范围是（ ）A．（-
，3）B．（-∞，-
）∪（3，+∞）C．（
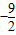，3）D．（-∞，
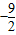）∪（3，+∞）
【答案】分析：先根据导数的图象可知函数是增函数，从而将f（2a+b）＜2=f（6）转化为：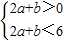
，再用线性规划，作出平面区域，
令t=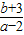
表示过定点（2，-3）的直线的斜率，通过数形结合法求解．
解答：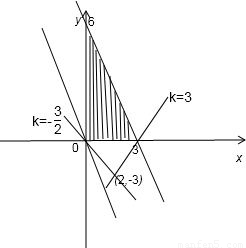
解：如图所示：f′（x）≥0在[-3，+∞）上恒成立
∴函数f（x）在[-3，0）是减函数，（0，+∞）上是增函数，
又∵f（2a+b）＜2=f（6）
∴
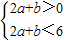
画出平面区域
令t=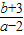
表示过定点（2，-3）的直线的斜率
如图所示：t∈（-∞，-
）∪（3，+∞）
故选B
点评：本题主要考查函数的单调性转化不等式，还考查了线性规划中的斜率模型．同时还考查了转化思想，数形结合思想．
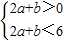，再用线性规划，作出平面区域，令t=
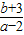表示过定点（2，-3）的直线的斜率，通过数形结合法求解．解答：
解：如图所示：f′（x）≥0在[-3，+∞）上恒成立∴函数f（x）在[-3，0）是减函数，（0，+∞）上是增函数，
又∵f（2a+b）＜2=f（6）
∴
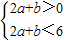
画出平面区域
令t=
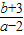表示过定点（2，-3）的直线的斜率如图所示：t∈（-∞，-
）∪（3，+∞）故选B
点评：本题主要考查函数的单调性转化不等式，还考查了线性规划中的斜率模型．同时还考查了转化思想，数形结合思想．
练习册系列答案
相关题目
