题目内容
在各项均不为零的等差数列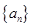
中，若a
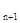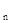
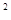- a
+ a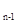
=0（n≥2），则S
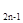-4n=（ ）
A -2 B 0 C 1 D 2
【答案】
A
【解析】
试题分析：因为a
- a
+ a
=0，所以a+ a=a，又因为数列是等差数列，所以a+ a=2a，所以a=2a，因为该数列各项都不为零，所以a=2，所以S
-4n=-2.
考点：本小题主要考查等差数列的性质和应用。
点评：解决此小题的关键是灵活应用等差数列的性质得出a=2，等差数列的性质是高考中一个热点问题，要给予充分的重视.
练习册系列答案
相关题目
中，若
，则
（ ）
Ｂ．
Ｃ．
Ｄ．
中，若
，则
（ ）
Ｂ．
Ｃ．
Ｄ．