题目内容
如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，
．
（1）求二面角A﹣DF﹣B的大小；
（2）在线段AC上找一点P，使PF与AD所成的角为60°，试确定点P的位置．
．（1）求二面角A﹣DF﹣B的大小；
（2）在线段AC上找一点P，使PF与AD所成的角为60°，试确定点P的位置．
解：（1）以
为正交基底，建立空间直角坐标系，则
，
∴面ADF的法向量
=（1，0，0），
，
=（
，0，1）．
设面DFB法向量
，则
，
所以
，
令a=1，得
，
∴
，
∴二面角A﹣DF﹣B的大小60°
（2）设
，
∴
，
∵
，
∴
，
解得
故存在满足条件的点P为AC的中点．
为正交基底，建立空间直角坐标系，则，∴面ADF的法向量
=（1，0，0），，=（，0，1）．设面DFB法向量
，则，所以
，令a=1，得
，∴
，∴二面角A﹣DF﹣B的大小60°
（2）设
，∴
，∵
，∴
，解得
故存在满足条件的点P为AC的中点．
练习册系列答案
相关题目
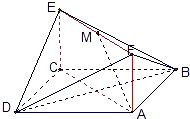如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=
如图，已知正方形ABCD的边长为1，过正方形中心O的直线MN分别交正方形的边AB，CD于M，N，则当
如图，已知正方形ABCD和梯形ACEF所在平面互相垂直，AB=2，AF=
如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，
（2012•深圳二模）如图，已知正方形ABCD在水平面上的正投影（投影线垂直于投影面）是四边形A′B′C′D′，其中A与A'重合，且BB′＜DD′＜CC′．