题目内容
已知
，若f（x）=ax2-2x+1在[1，3]上的最大值为M（a），最小值为N（a），已知g（a）=M（a）-N（a）．
（1）求g（a）的函数表达式．
（2）判断g（a）在
上的单调性，并证明．
（3）求出函数y=g（a）在上的值域．
解：（1）函数f（x）=ax2-2x+1的对称轴为x=
∵，
∴∈[1，
]
∵函数f（x）=ax2-2x+1开口向上，对称轴x=∈[1，]
∴g（a）=M（a）-N（a）=f（3）-f（）=9a+-6．
（2）g′（a）=9-
当a∈时，g′（a）=9-＞0
∴g（a）在上单调递增
（3）由（2）可知g（a）在上单调递增
∴g（a）min=g（
）=，g（a）max=g（1）=4
则函数y=g（a）在上的值域为[，4]
分析：（1）先判定二次函数的对称轴的范围，然后根据二次函数的性质可求出该函数的最值，从而求出g（a）的函数表达式．
（2）先求导函数，然后判定导函数在上的符号，从而确定函数的单调性；
（3）利用（2）的结论可求出函数的最值，从而得到函数的值域．
点评：本题主要考查了二次函数的性质，以及利用导数研究函数的单调性和值域，同时考查了计算能力，属于中档题．
∵
，∴
∈[1，]∵函数f（x）=ax2-2x+1开口向上，对称轴x=
∈[1，]∴g（a）=M（a）-N（a）=f（3）-f（
）=9a+-6．（2）g′（a）=9-
当a∈
时，g′（a）=9-＞0∴g（a）在
上单调递增（3）由（2）可知g（a）在
上单调递增∴g（a）min=g（
）=，g（a）max=g（1）=4则函数y=g（a）在
上的值域为[，4]分析：（1）先判定二次函数的对称轴的范围，然后根据二次函数的性质可求出该函数的最值，从而求出g（a）的函数表达式．
（2）先求导函数，然后判定导函数在
上的符号，从而确定函数的单调性；（3）利用（2）的结论可求出函数的最值，从而得到函数的值域．
点评：本题主要考查了二次函数的性质，以及利用导数研究函数的单调性和值域，同时考查了计算能力，属于中档题．
练习册系列答案
相关题目
若f（x）＞3，则x的取值范围是（ ）
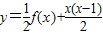的反函数为p（x），t（x）=p（x）（1-x），求函数t（x）的最大值；
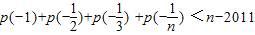恒成立？若存在，请找出一个满足条件的N的值，并给以说明；若不存在，请说明理由．
，若f（x）=ax2-2x+1在区间[1，3]上的最大值为M（a），最小值为N（a），记g（a）=M（a）-N（a）．
都有kg（a）-1＜0成立，求实数k的取值范围．
若f（x）＞3，则x的取值范围是（ ）