题目内容
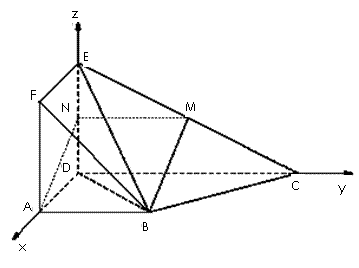
(12分)如图正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD, AB//CD,AB=AD=2,CD=4,M为CE的中点。
(I)求证:BM//平面ADEF;
(II)求证:平面![]() 平面BEC;
平面BEC;
(III)求平面BEC与平面ADEF所成锐二面角的余弦值。

(1)证明:取DE中点N,连结MN,AN
 |
在ΔEDC中,M、N分别为EC, ED的中点,所以MN//CD,且MN=![]() CD.
CD.
由已知AB//CD, AB=![]() CD,所以MN//AB, 且MN=AB。
CD,所以MN//AB, 且MN=AB。
所以四边形ABMN为平行四边形,所以BM//AN
又因为AN![]() 平面ADEF,
平面ADEF,
且BM![]() 平面ADEF,
平面ADEF,
所以BM//平面ADEF。……(4分)
(2)证明:
在正方形ADEF中,ED⊥AD,
又因为平面ADEF⊥平面ABCD,
且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD,所以ED⊥BC.
在直角梯形ABCD中,
AB=AD=2, CD=4,可得BC=![]()
在ΔBCD中,BD=BC=![]() ,CD=4,
,CD=4,
所以BC⊥BD。
所以BC⊥平面BDE,又因为BC![]() 平面BCE,
平面BCE,
所以平面BDE⊥平面BEC。 ……(9分)
(3)由(2)知ED⊥平面ABCD,且AD⊥CD。
以D为原点,DA, DC, DE所在直线为x,y,z轴,建立空间直角坐标系。
B(2,2,0), C(0,4,0), E(0,0,2),平面ADEF的一个法向量为m=(0,1,0).
设n=(x,y,z)为平面BEC的一个法向量,因为![]()
![]()
所以n=(1,1,2)为平面BEC的一个法向量
设平面BEC与平面ADEF所成锐二面角为![]()
则![]()
所以平面BEC与平面ADEF所成锐二面角为余弦值为![]()

练习册系列答案
相关题目
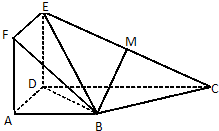 如图正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,
如图正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,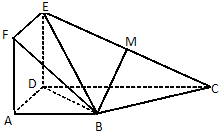
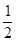 CD=2,点M在线段EC上.
CD=2,点M在线段EC上.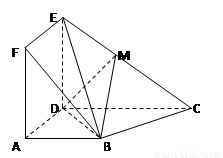
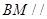 面
面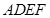 ;
;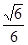 时,求三棱锥M-BDE的体积.
时,求三棱锥M-BDE的体积.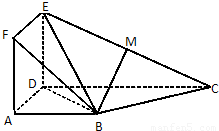 如图正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,
如图正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,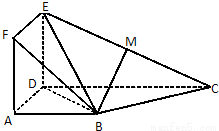 如图正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,
如图正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,