题目内容
如图,在四棱锥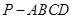 中,
中,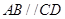 ,
,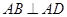 ,
,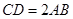 ,平面
,平面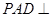 底面
底面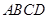 ,
,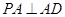 .
. 和
和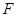 分别是
分别是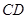 和
和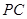 的中点,求证:
的中点,求证:
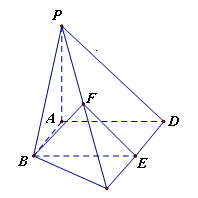
(Ⅰ)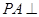 底面
底面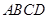 ;
;
(Ⅱ)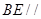 平面
平面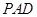 ;
;
(Ⅲ)平面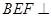 平面
平面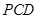 .
.
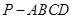 中,
中,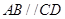 ,
,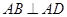 ,
,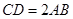 ,平面
,平面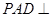 底面
底面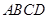 ,
,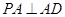 .
.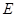 和
和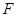 分别是
分别是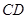 和
和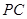 的中点,求证:
的中点,求证:
(Ⅰ)
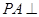 底面
底面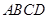 ;
;(Ⅱ)
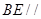 平面
平面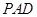 ;
;(Ⅲ)平面
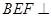 平面
平面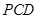 .
.把平面与平面垂直转化为直线和平面垂直是常见的转化.要证直线和平面垂直,依据相关判定定理转化为证明直线和直线垂直.要证直线和平面平行,可以利用直线和平面平行的判定定理完成。证明平面与平面垂直,需要在一个平面内找到一条和另一个平面垂直的直线,依据平面与平面垂直的判定定理。
(Ⅰ)因为平面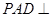 底面
底面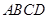 ,且
,且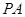 垂直于这两个平面的交线
垂直于这两个平面的交线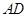 ,
,
所以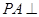 底面
底面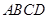 .
.
(Ⅱ)因为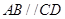 ,
,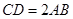 ,
, 是
是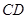 的中点,
的中点,
所以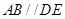 ,且
,且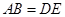 .
.
所以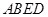 为平行四边形.
为平行四边形.
所以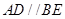 ,.
,.
又因为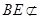 平面
平面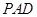 ,
,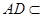 平面
平面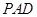 ,
,
所以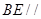 平面
平面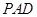 .
.
(Ⅲ)因为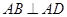 ,并且
,并且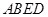 为平行四边形,
为平行四边形,
所以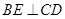 ,
,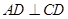 .
.
由(Ⅰ)知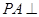 底面
底面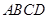 ,
,
所以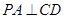 ,
,
所以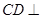 平面
平面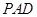 .
.
所以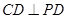 .
.
因为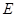 和
和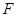 分别是
分别是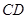 和
和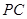 的中点,
的中点,
所以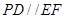 .
.
所以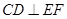 .
.
所以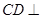 平面
平面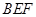 .
.
所以平面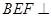 平面
平面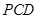 .
.
【考点定位】本题考查了直线和平面平行、垂直的判定定理,平面与平面垂直的判定定理和性质定理,考查推理论证能力.
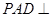 底面
底面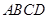 ,且
,且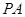 垂直于这两个平面的交线
垂直于这两个平面的交线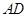 ,
, 所以
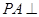 底面
底面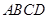 .
.(Ⅱ)因为
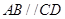 ,
,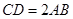 ,
,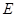 是
是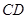 的中点,
的中点,所以
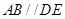 ,且
,且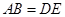 .
.所以
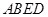 为平行四边形.
为平行四边形.所以
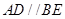 ,.
,.又因为
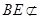 平面
平面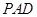 ,
,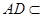 平面
平面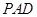 ,
,所以
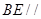 平面
平面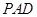 .
.(Ⅲ)因为
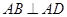 ,并且
,并且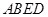 为平行四边形,
为平行四边形,所以
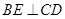 ,
,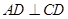 .
.由(Ⅰ)知
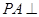 底面
底面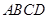 ,
,所以
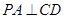 ,
,所以
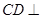 平面
平面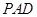 .
.所以
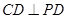 .
.因为
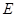 和
和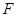 分别是
分别是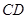 和
和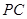 的中点,
的中点,所以
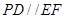 .
.所以
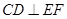 .
.所以
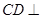 平面
平面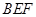 .
.所以平面
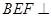 平面
平面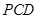 .
.【考点定位】本题考查了直线和平面平行、垂直的判定定理,平面与平面垂直的判定定理和性质定理,考查推理论证能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
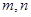 是两条不同的直线,
是两条不同的直线,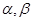 是两个不同的平面,则下列正确命题的序号是 .
是两个不同的平面,则下列正确命题的序号是 .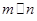 ,
,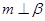 , 则
, 则 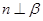 ; ②.若
; ②.若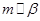 ,则
,则 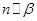 ;
;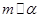 ,
,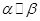 ; ④.若
; ④.若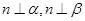 ,则
,则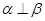 .
. 中,面对角线
中,面对角线 与体对角线
与体对角线 所成角等于
所成角等于
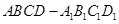 的棱长为1,
的棱长为1,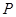 为
为 的中点,
的中点,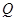 为线段
为线段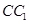 上的动点,过点
上的动点,过点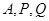 的平面截该正方体所得的截面记为
的平面截该正方体所得的截面记为 ,则下列命题正确的是 (写出所有正确命题的编号).
,则下列命题正确的是 (写出所有正确命题的编号).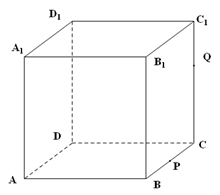
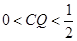 时,
时,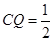 时,
时,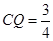 时,
时,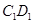 的交点
的交点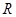 满足
满足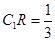
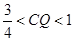 时,
时,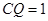 时,
时,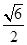
 与共面的直线m,n,下列命题为真命题的是 ( )
与共面的直线m,n,下列命题为真命题的是 ( ) ,
, ,则
,则 //
//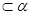 ,n//
,n//



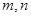 和平面
和平面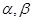 ,有如下四个命题:
,有如下四个命题: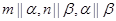 ,则
,则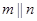 ;
;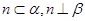 ,则
,则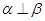 ;
;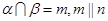 ,则
,则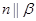 且
且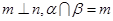 ,则
,则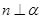 或
或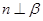 。其中真命题的个数是 .
。其中真命题的个数是 .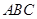 —
—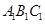 ,侧面
,侧面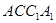 与底面
与底面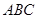 垂直,∠
垂直,∠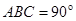 ,
,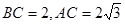 ,且
,且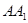 ⊥
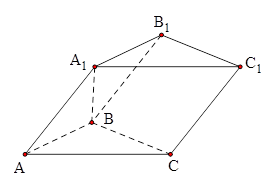
⊥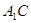 ,
,
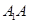 与平面
与平面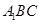 是否垂直,并说明理由;
是否垂直,并说明理由;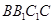 与底面
与底面