题目内容
【题目】一个酒杯的轴截面是一条抛物线的一部分，它的方程是x2=2y，y∈[0，10]，在杯内放入一个清洁球，要求清洁球能擦净酒杯的最底部（如图），则清洁球的最大半径为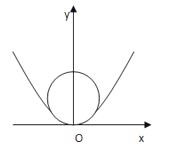 
【答案】1
【解析】设小球圆心（0，y0）
抛物线上点（x，y）
点到圆心距离平方为：
r2=x2+（y﹣y0）2=2y+（y﹣y0）2=y2+2（1﹣y0）y+y02
若r2最小值在（0，0）时取到，则小球触及杯底
故此二次函数的对称轴位置应在y轴的左侧，所以1﹣y0≥0y0≤1，
所以0＜r≤1，从而清洁球的半径r的范围为 0＜r≤1
则清洁球的最大半径为 1
故答案为：1．
设小球圆心（0，y0） 抛物线上点（x，y），求得点到球心距离r平方的表达式，进而根据若r2最小值在（0，0）时取到，则小球触及杯底，需1﹣y0≥0 进而求得r的范围．
练习册系列答案
相关题目
