Question

如图，四棱锥P—ABCD底面为正方形，DP⊥平面ABCD，AB=2，E为BP中点，异面直线DP、AE所成角的余弦为.

（1）求DP的长；

（2）在平面PAD内求一点F，使EF⊥平面PBC.

Answer 1

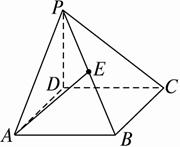
思路分析：设定适当的坐标，利用空间向量的垂直证明EF垂直平面PBC中的两方向不同的向量.

解：（1）令=2i、=2j、=2mk，其中{i,j,k}为单位正交基底，易得点E（1，1,m），P(0,0,2m)，A(2,0,0),=(-1,1,m),

∴.

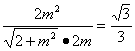∴m=1,即所求DP=2.

（2）设点F(x,0,z)，即=(x-1,-1,z-1).

则·=（x-1，-1,z-1）·(2,0,0)=2(x-1)=0.∴x=1.

同理·=0.

∴z=0，即所求点为F(1,0,0)，为AD中点.