题目内容
(江西卷理)(本小题满分12分)
 已知点
已知点![]() 为双曲线
为双曲线![]() (
(![]() 为正常数)上任一点,
为正常数)上任一点,![]() 为双曲线的右焦点,过
为双曲线的右焦点,过![]() 作右准线的垂线,垂足为
作右准线的垂线,垂足为![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于
轴于![]() .
. ![]()
![]()
(1) 求线段![]()
![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2) 设轨迹![]() 与
与![]() 轴交于
轴交于![]() 两点,在
两点,在![]() 上任取一点
上任取一点![]() ,直线
,直线![]() 分别交
分别交![]() 轴于
轴于![]() 两点.求证:以
两点.求证:以![]() 为直径的圆过两定点.
为直径的圆过两定点.
![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .,
.,![]()
解析:
(1) 解 由已知得![]() ,则直线
,则直线![]() 的方程为:
的方程为:![]() ,
,
令![]() 得
得![]() ,即
,即![]() ,
,
设![]() ,则
,则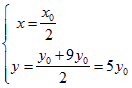 ,即
,即 代入
代入![]() 得:
得:![]() ,
,
即![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
. ![]()
![]()
(2) 证明 在![]() 中令
中令![]() 得
得![]() ,则不妨设
,则不妨设![]() ,
,
于是直线![]() 的方程为:
的方程为:![]() ,
,
![]() 直线
直线![]() 的方程为:
的方程为:![]() ,
,
则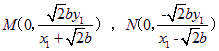 ,
,
则以![]() 为直径的圆的方程为:
为直径的圆的方程为: 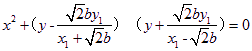
![]() ,
,
令![]() 得:
得:![]() ,而
,而![]() 在
在![]() 上,则
上,则![]() ,
,
于是![]() ,即以
,即以![]() 为直径的圆过两定点
为直径的圆过两定点![]() .
.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目