题目内容
函数f (x)=log5(x2+1), x∈[2, +∞ 的反函数是 ( )
的反函数是 ( )
 的反函数是 ( )
的反函数是 ( )A.g (x)= ( x≥0) ( x≥0) | B.g (x)= ( x≥1) ( x≥1) |
C.g (x)= ( x≥0) ( x≥0) | D.g (x)= ( x≥1) ( x≥1) |
D
解法一:令y=log5(x2+1),可得5y= x2+1,∴x2=5y-1, 又∵x∈[2, +∞ 即x>0.
即x>0.
∴x= .∵x≥2,∴x2+1≥5,y=log5(x2+1)≥1.
.∵x≥2,∴x2+1≥5,y=log5(x2+1)≥1.
∴函数f (x)=log5(x2+1), x∈[2, +∞ 的反函数是g (x)=
的反函数是g (x)= ( x≥1)。故选D.
( x≥1)。故选D.
解法二:∵x≥2,∴x2+1≥5,原函数y=log5(x2+1)≥1.由原函数和反函数中x,y的对应关系知反函数中的x≥1,排除A、 C,而B中 y= >2, 排除B. 故选D.
>2, 排除B. 故选D.
解法三:原函数f (x)=log5(x2+1)经过点(2,1),反函数y=g (x)经过点(1,2),以 (1,2)点代入排除A、B,又原函数中y≥1,从而反函数中x≥1,排除 C,故选D.
 即x>0.
即x>0.∴x=
 .∵x≥2,∴x2+1≥5,y=log5(x2+1)≥1.
.∵x≥2,∴x2+1≥5,y=log5(x2+1)≥1.∴函数f (x)=log5(x2+1), x∈[2, +∞
 的反函数是g (x)=
的反函数是g (x)= ( x≥1)。故选D.
( x≥1)。故选D.解法二:∵x≥2,∴x2+1≥5,原函数y=log5(x2+1)≥1.由原函数和反函数中x,y的对应关系知反函数中的x≥1,排除A、 C,而B中 y=
 >2, 排除B. 故选D.
>2, 排除B. 故选D. 解法三:原函数f (x)=log5(x2+1)经过点(2,1),反函数y=g (x)经过点(1,2),以 (1,2)点代入排除A、B,又原函数中y≥1,从而反函数中x≥1,排除 C,故选D.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 的图象上一点
的图象上一点 及邻近一点
及邻近一点 ,则
,则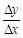 等于( )
等于( )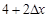

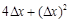
 是函数
是函数 的反函数,则使
的反函数,则使 成立的x的取值范围为( )
成立的x的取值范围为( )



 的反函数是( )
的反函数是( )



 的反函数为
的反函数为 ,则满足
,则满足 的x的集合是
的x的集合是 是方程
是方程 的解,
的解, 是
是 的解,
的解, 的值为( )
的值为( )



 (x
(x 0)的反函数是( )
0)的反函数是( ) (x
(x 0)
0) (x
(x 0)
0)