题目内容
有四个关于三角函数的命题：
（1）P1：?x∈R，sin2
+cos2=
；
（2）P2：?x、y∈R，sin（x-y）=sinx-siny；
（3）P3：?x∈[0，π]，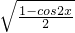
=sinx；
（4）P4：sinx=cosy?x+y=
，其中真命题的是________．
解：（1）：?x∈R，sin2+cos2=； 不满足同角三角函数的基本关系式的平方关系式，所以不正确；
（2）：?x、y∈R，sin（x-y）=sinx-siny；例如x=1，y=0，左式成立，所以（2）正确；
（3）：?x∈[0，π]，=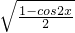
=sinx；正确．
（4）：sinx=cosy?sinx=sin（
），x=
y+2kπ或x=
，k∈Z，所以（4）不正确．
真命题有（2）（3）．
故答案为：（2）（3）．
分析：利用同角三角函数的基本关系式判断（1）的正误；
利用特例判断（2）的正误；
利用二倍角公式化简判断（3）的正误；
利用三角方程求出x，y的关系，判断（4）的正误；
点评：本题考查特称命题，全称命题，命题的真假判断与应用，考查基本知识的应用．
+cos2=； 不满足同角三角函数的基本关系式的平方关系式，所以不正确； （2）：?x、y∈R，sin（x-y）=sinx-siny；例如x=1，y=0，左式成立，所以（2）正确；
（3）：?x∈[0，π]，
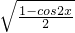==sinx；正确． （4）：sinx=cosy?sinx=sin（
），x=y+2kπ或x=，k∈Z，所以（4）不正确．真命题有（2）（3）．
故答案为：（2）（3）．
分析：利用同角三角函数的基本关系式判断（1）的正误；
利用特例判断（2）的正误；
利用二倍角公式化简判断（3）的正误；
利用三角方程求出x，y的关系，判断（4）的正误；
点评：本题考查特称命题，全称命题，命题的真假判断与应用，考查基本知识的应用．
练习册系列答案
相关题目