题目内容
已知函数f（x）=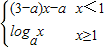
是（-∞，+∞）上的递增函数，则实数a的取值范围是（ ）A．（1，+∞）
B．（-∞，3）
C．[
，3）D．（1，3）
【答案】分析：本题考查的是分段函数和函数单调性的综合类问题．在解答时，首先得保证函数在各段上是增函数，然后保证x=1时x＜1对应的上限要小于等于x≥1时函数对应的下限．解不等式进而获得问题的解答．
解答：解：由题意：函数f（x）=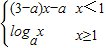
是（-∞，+∞）上的递增函数，
所以必有：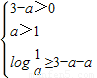
，解得：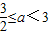
，
故选C．
点评：本题考查的是分段函数和函数单调性的综合类问题．在解答的过程当中充分体现了分段函数的思想、解不等式的思想以及数形结合的思想．值得同学们体会和反思．
解答：解：由题意：函数f（x）=
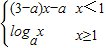是（-∞，+∞）上的递增函数，所以必有：
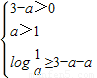，解得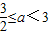：，故选C．
点评：本题考查的是分段函数和函数单调性的综合类问题．在解答的过程当中充分体现了分段函数的思想、解不等式的思想以及数形结合的思想．值得同学们体会和反思．
练习册系列答案
相关题目
已知函数f（x+1）是偶函数，当x2＞x1＞1时，[f（x2）-f（x1）]（ x2-x1）＞0恒成立，设a=f （-
），b=f（2），c=f（3），则a，b，c的大小关系为（ ）
| 1 |
| 2 |
| A、b＜a＜c |
| B、c＜b＜a |
| C、b＜c＜a |
| D、a＜b＜c |