题目内容
12.设自然数n≥3,证明:可将一个正三角形分成n个等腰三角形.分析 设D,E,F是正三角形ABC的边BC,CA,AB上的中点,O为中心.1.连AO,BO,CO,则将正三角形ABC分为三个相等的顶角为120°的等腰三角形;
2.连AD,DE,DF.则△ADE,△ADF是相等的顶角为120°的等腰三角形△BDF,△CDE是相等的正三角形;这样将正三角形ABC分为四个等腰三角形;
3.在AD上取一点H,使DH=$\frac{1}{2}BC$,则△BHC是等腰直角三角形,分别在CA,AB上取一点P与Q,使∠APH=∠AQH=30°.则△APH,△AQH是相等的顶角为120°的等腰三角形,△PCH,△QBH是相等的顶角为150°的等腰三角形,这样将正三角形ABC分为五个等腰三角形;
4.在第三种情况下,我们只需分割等腰直角三角形BHC,那可得出所有分割.
解答 解:设D,E,F是正三角形ABC的边BC,CA,AB上的中点,O为中心.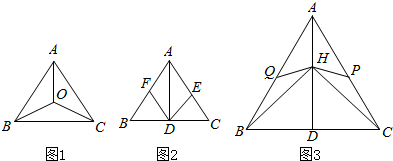
1.连AO,BO,CO,则将正三角形ABC分为三个相等的顶角为120°的等腰三角形;
2.连AD,DE,DF.则△ADE,△ADF是相等的顶角为120°的等腰三角形△BDF,△CDE是相等的正三角形;
这样将正三角形ABC分为四个等腰三角形;
3.在AD上取一点H,使DH=$\frac{1}{2}BC$,则△BHC是等腰直角三角形,分别在CA,AB上取一点
P与Q,使∠APH=∠AQH=30°.则
△APH,△AQH是相等的顶角为120°的等腰三角形,
△PCH,△QBH是相等的顶角为150°的等腰三角形,
这样将正三角形ABC分为五个等腰三角形;
4.在第三种情况下,我们只需分割等腰直角三角形BHC,那可得出所有分割.下面利用数学归纳法证明:只需分割等腰直角三角形BDH,那可得出所有分割.
(1)当n=1时,△BDH是等腰直角三角形,取BH的中点M1,连接DM1,则Rt△BDM1,Rt△DHM1都是等腰直角三角形.即由一个等腰直角三角形可以分割成两个等腰直角三角形.
(2)假设由n个等腰直角三角形可以分割成n+1个等腰直角三角形.
下面证明:由n+1个等腰直角三角形可以分割成n+2个等腰直角三角形,只需将其中的一个等腰直角三角形分割成两个等腰直角三角形即可,这个由(1)成立.
综上可知:上述结论成立.
因此可将一个正三角形分成n个等腰三角形.
点评 本题考查了将一个正三角形分成n个等腰三角形的问题、正三角形的性质、等腰直角三角形的性质、首项归纳法,考查了数形结合方法、推理能力与计算能力,属于难题.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案| A. | (-∞,0] | B. | [2,+∞) | C. | (-∞,0]∪[2,+∞) | D. | [0,2] |
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 不确定 |
 如图,在四棱柱ABCD-A1B1C1D1中,AB∥C1D1,AB1⊥BC,且AA1=AB.
如图,在四棱柱ABCD-A1B1C1D1中,AB∥C1D1,AB1⊥BC,且AA1=AB.