题目内容
【题目】设函数
．
（1）关于
的不等式
对一切
恒成立，求实数
的取值范围；
（2）解关于的不等式
；
（3）函数
在区间
上有零点，求实数的取值范围．
【答案】（1）
；（2）见解析；（3）
.
【解析】
（1）
对一切
恒成立，即
，恒成立，所以
，解得即可；
（2）对判别式讨论大于0，等于0，小于0，再由二次不等式的解法，即可得到；
（3）要使函数在
有零点，只需考虑
的符号和对称轴的位置及端点的函数值的符号以及零点存在定理和运用，列出不等式组，解出即可得到范围．
（1）由题意得，
对一切恒成立，
即
，恒成立，
所以
，即
，
解得，
，
所以实数的取值范围；
（2）由
，得，
，
即
，
其中
，
当
即
时，不等式无实数解；
当
，即
或
时，
设
，
，
则
，
综上所述，当时，不等式无解；
当或时，不等式的解集为
；
（3）要使函数
在区间上
上有零点，
须
或
，或
，
即
或
，
解得，
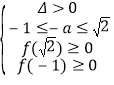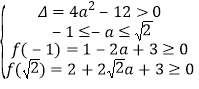或
，
综上所述，实数的取值范围
．
练习册系列答案
相关题目
【题目】有一个同学家开了一个奶茶店，他为了研究气温对热奶茶销售杯数的影响，从一季度中随机选取5天，统计出气温与热奶茶销售杯数，如表：
气温 | 0 | 4 | 12 | 19 | 27 |
热奶茶销售杯数 | 150 | 132 | 130 | 104 | 94 |
（Ⅰ）求热奶茶销售杯数关于气温的线性回归方程
（
精确到0.1），若某天的气温为
，预测这天热奶茶的销售杯数；
（Ⅱ）从表中的5天中任取两天，求所选取两天中至少有一天热奶茶销售杯数大于130的概率．
参考数据：
，
.
参考公式：
，
．
