题目内容
若函数
上单调递减，则实数a的取值范围是________．
[9，12]
分析：将原函数
看成是函数：y=log
μ，μ=x3-ax的复合函数，利用对数函数与三次函数的单调性来研究即可．注意对数的真数必须大于0．
解答：设μ=x3-ax．
则原函数是函数：y=logμ，μ=x3-ax的复合函数，
因y=logμ在（0，+∞）上是减函数，
根据复合函数的单调性，得
函数的单调减区间是函数μ=x3-ax的单调增区间，
∴μ′=3x2-a≥0在（-3，-2）恒成立，即a≤3x2在（-3，-2）恒成立，
∴a≤3×（-2）2=12
且μ=（-3）3-a×（-3）≥0?a≥9，
∴9≤a≤12．
故答案为：[9，12]．
点评：本题考查复合函数的单调性、导数的应用，是基础题．复合函数的单调性一般是看函数包含的两个函数的单调性（1）如果两个都是增的，那么函数就是增函数 （2）一个是减一个是增，那就是减函数 （3）两个都是减，那就是增函数．
分析：将原函数
看成是函数：y=logμ，μ=x3-ax的复合函数，利用对数函数与三次函数的单调性来研究即可．注意对数的真数必须大于0．解答：设μ=x3-ax．
则原函数是函数：y=log
μ，μ=x3-ax的复合函数，因y=log
μ在（0，+∞）上是减函数，根据复合函数的单调性，得
函数
的单调减区间是函数μ=x3-ax的单调增区间，∴μ′=3x2-a≥0在（-3，-2）恒成立，即a≤3x2在（-3，-2）恒成立，
∴a≤3×（-2）2=12
且μ=（-3）3-a×（-3）≥0?a≥9，
∴9≤a≤12．
故答案为：[9，12]．
点评：本题考查复合函数的单调性、导数的应用，是基础题．复合函数的单调性一般是看函数包含的两个函数的单调性（1）如果两个都是增的，那么函数就是增函数 （2）一个是减一个是增，那就是减函数 （3）两个都是减，那就是增函数．
练习册系列答案
精英口算卡系列答案
相关题目
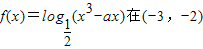上单调递减，则实数a的取值范围是 ．