题目内容
设函数f(x)=cos2x+θcosx+sinθ,x∈[- ,
, ],是否存在θ∈[-
],是否存在θ∈[- ,
, ],使得f(x)的最小值是-
],使得f(x)的最小值是- -cos(θ+
-cos(θ+ ),若存在,试求出θ,若不存在,说明理由.
),若存在,试求出θ,若不存在,说明理由.
解:设cosx=t则f(x)=y=t2+θt+sinθ,t∈[- ,1]
,1]
y=t2+θt+sinθ开口向上,对称轴t=- ,-
,- ∈[-
∈[- ,
, ]
]
1当- ∈[-
∈[- ,
, ]即-
]即- ≤θ≤1时
≤θ≤1时
ymin=y(- )=
)= -
- +sinθ=-
+sinθ=- +sinθ
+sinθ
由- +sinθ=-
+sinθ=- -cos(θ+
-cos(θ+ )=-
)=- +sinθ?θ2=2?θ=±
+sinθ?θ2=2?θ=±
又- ≤θ1∴此时θ=-
≤θ1∴此时θ=-
2当- ∈[-
∈[- ,-
,- ],即1<θ≤
],即1<θ≤ 时,
时,
y关于t的函数在[- ,1]上是增函数
,1]上是增函数
ymin=y(- )=
)= -
- θ+sinθ
θ+sinθ
- ,
, ,
,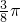 ,
, ,
, 由
由 -
- θ+sinθ=-
θ+sinθ=- -cos(θ+
-cos(θ+ )
)
? θ=
θ= ?θ-
?θ- ∈(1,
∈(1, )合题意
)合题意
∴存在θ=- ,或θ=
,或θ= .
.
分析:令cosx=t将三角函数转化为二次函数的最值,求出二次函数的对称轴,讨论对称轴与定义域的关系,求出二次函数的最小值,列出关于θ的方程,求出θ.
点评:本题考查通过换元将三角函数的最值问题转化为二次函数的最值问题,注意:换元要注意新变量的范围;求二次函数的最值关键是弄清对称轴与给定区域的关系.
 ,1]
,1]y=t2+θt+sinθ开口向上,对称轴t=-
 ,-
,- ∈[-
∈[- ,
, ]
]1当-
 ∈[-
∈[- ,
, ]即-
]即- ≤θ≤1时
≤θ≤1时ymin=y(-
 )=
)= -
- +sinθ=-
+sinθ=- +sinθ
+sinθ由-
 +sinθ=-
+sinθ=- -cos(θ+
-cos(θ+ )=-
)=- +sinθ?θ2=2?θ=±
+sinθ?θ2=2?θ=±
又-
 ≤θ1∴此时θ=-
≤θ1∴此时θ=-
2当-
 ∈[-
∈[- ,-
,- ],即1<θ≤
],即1<θ≤ 时,
时,y关于t的函数在[-
 ,1]上是增函数
,1]上是增函数ymin=y(-
 )=
)= -
- θ+sinθ
θ+sinθ-
 ,
, ,
,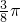 ,
, ,
, 由
由 -
- θ+sinθ=-
θ+sinθ=- -cos(θ+
-cos(θ+ )
)?
 θ=
θ= ?θ-
?θ- ∈(1,
∈(1, )合题意
)合题意∴存在θ=-
 ,或θ=
,或θ= .
.分析:令cosx=t将三角函数转化为二次函数的最值,求出二次函数的对称轴,讨论对称轴与定义域的关系,求出二次函数的最小值,列出关于θ的方程,求出θ.
点评:本题考查通过换元将三角函数的最值问题转化为二次函数的最值问题,注意:换元要注意新变量的范围;求二次函数的最值关键是弄清对称轴与给定区域的关系.

练习册系列答案
相关题目