题目内容
若O,A,B三点不共线,证明P,A,B三点共线的充要条件是存在实数λ,μ,使得
思路分析:由于P,A,B三点中任意两点都可以构造一个向量,则可利用两个向量共线的充要条件再作适当的变形就可以证得结论.
证明:必要性.
若P,A,B三点共线,则![]() 与
与![]() 共线.
共线.
则有![]() (t∈R),即
(t∈R),即![]() .
.
所以![]() .
.
令λ=1-t,μ=t,则λ+μ=1.
所以存在实数λ,μ,使得![]() ,且λ+μ=1,λ,μ∈R.
,且λ+μ=1,λ,μ∈R.
充分性.
若存在实数λ,μ,使得![]() ,且λ+μ=1,λ,μ∈R,
,且λ+μ=1,λ,μ∈R,
则有![]() ,
,
即![]() .∴
.∴![]() .
.
所以![]() 与
与![]() 共线.
共线.
又![]() 与
与![]() 有相同的起点,所以P,A,B三点共线.
有相同的起点,所以P,A,B三点共线.
方法归纳 所谓要证命题的必要性成立,就是由命题的结论成立,推证命题的题设(条件)成立;所谓要证命题的充分性成立,就是由命题的条件成立,推证结论成立.
深化升华 证明充分性与必要性的关键是分清题设(条件)与结论,可将它们与命题联系起来,即若原命题成立,则题设是结论成立的充分条件;若逆命题成立,则题设是结论成立的必要条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
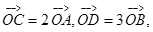 ,设
,设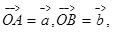
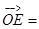 .(用向量
.(用向量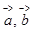 表示)
表示)