题目内容
(本小题满分12分)
已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(1)因为函数![]() 是奇函数,所以有
是奇函数,所以有![]() 即
即![]() 解得
解得![]()
从而有![]() ………… 2分
………… 2分
又由![]() 知
知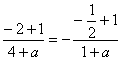 ,得
,得![]() ……… 4分
……… 4分
(2)由![]()
由上式易知,函数![]() 在
在![]() 是单调递减函数……… 6分
是单调递减函数……… 6分
又函数![]() 是奇函数,从而不等式
是奇函数,从而不等式![]() 等价于
等价于
![]()
再由函数![]() 的单调性知,上述不等式等价于
的单调性知,上述不等式等价于![]() ……… 9分
……… 9分
即对一切![]() ,不等式
,不等式![]() 总成立
总成立
即![]() 在
在![]() 恒成立
恒成立
考察函数![]()
![]() 是增函数
是增函数
所以![]()
所以满足题意的实数![]() 的取值范围是
的取值范围是![]() ………12
………12

练习册系列答案
相关题目