题目内容
在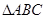 中,
中,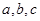 分别为内角A,B,C所对的边长,
分别为内角A,B,C所对的边长,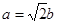 ,
,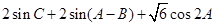
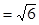 .
.
(1)求角B的大小。
(2)若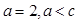 求
求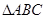 的面积
的面积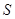 .
.
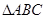 中,
中,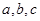 分别为内角A,B,C所对的边长,
分别为内角A,B,C所对的边长,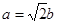 ,
,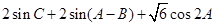
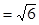 .
.(1)求角B的大小。
(2)若
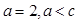 求
求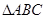 的面积
的面积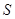 .
.(1)角B为 ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:本题考查解三角形中的正弦定理的运用以及运用三角公式进行三角变换的能力和三角形面积公式,考查基本的运算能力.第一问,由正弦定理得
 ,再利用两角和与差的正弦公式和倍角公式化简第二个已知条件,两式结合,得
,再利用两角和与差的正弦公式和倍角公式化简第二个已知条件,两式结合,得 ,注意是在三角形中求角
,注意是在三角形中求角 ;第二问,结合第一问的结论,得
;第二问,结合第一问的结论,得 ,通过边的大小确定角
,通过边的大小确定角 的大小,已知有
的大小,已知有 边的长度,要求三角形面积还需求
边的长度,要求三角形面积还需求 角,由
角,由 角求
角求 角,从而求出
角,从而求出 ,所以代入三角形面积公式中即可.
,所以代入三角形面积公式中即可.试题解析:(1)由正弦定理及已知可得
 1分
1分 得
得 4分
4分所以
 解得
解得 又因为在
又因为在 ABC中
ABC中所以角B为
 6
6 分
分(2)由(1)知
 又因为
又因为 所以
所以 7分
7分所以


 9分
9分 12分
12分
练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 中,
中, 分别是内角
分别是内角 所对的边,且
所对的边,且 。
。 的大小;
的大小;  ,且
,且 ,求
,求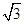 sin
sin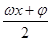 cos
cos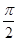 ).其图象的两个相邻对称中心的距离为
).其图象的两个相邻对称中心的距离为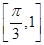 .
.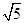 ,S△ABC=2
,S△ABC=2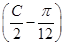 =
=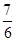 ,求c的值.
,求c的值. 中,
中, 依次成等比数列,则角
依次成等比数列,则角 的取值范围是 .
的取值范围是 . 中,
中, ,则此三角形解的情况是( )
,则此三角形解的情况是( ) ,b=
,b= ,则B=
,则B=  中,若
中,若 ,则
,则 .
. 中,角
中,角 所对的边分别为
所对的边分别为 ,若
,若 ,则
,则 等于 ( )
等于 ( )



 中,若
中,若 =
= °, ∠B=
°, ∠B= °,BC =
°,BC = ,则AC =
,则AC =