题目内容
已知点A的坐标为![]() ,直线
,直线![]() 的方程为3
的方程为3![]() +
+![]() -2=0,求:
-2=0,求:
(1)点A关于直线![]() 的对称点A′的坐标; (2)直线
的对称点A′的坐标; (2)直线![]() 关于点A的对称直线
关于点A的对称直线![]() 的方程.
的方程.
解析:(1)设点A′的坐标为(![]() ′,
′,![]() ′). 因为点A与A′关于直线
′). 因为点A与A′关于直线![]() 对称,所以AA′⊥
对称,所以AA′⊥![]() ,且AA′的中点在
,且AA′的中点在![]() 上,而直线
上,而直线![]() 的斜率是-3,所以
的斜率是-3,所以![]() ′=
′=![]() .
.
又因为![]() =
=![]() .
.
又直线![]() 的方程为3
的方程为3![]() +
+![]() -2=0,AA′中点坐标(
-2=0,AA′中点坐标(![]() ),所以3?
),所以3?![]() -2=0.
-2=0.
由①和②,解得![]() ′=2,
′=2,![]() ′=6. 所以A′点的坐标为(2,6).
′=6. 所以A′点的坐标为(2,6).
(2)关于点A对称的两直线![]() 与
与![]() 互相平行,于是可设
互相平行,于是可设![]() 的方程为3
的方程为3![]() +
+![]() +c=0. 在直线
+c=0. 在直线![]() 上任取一点M(0,2),其关于点A对称的点为M′(
上任取一点M(0,2),其关于点A对称的点为M′(![]() ′,
′,![]() ′),于是M′点在
′),于是M′点在![]() 上,且MM′的中点为点A,由此得
上,且MM′的中点为点A,由此得![]() ,即:
,即:![]() ′=-8,
′=-8,![]() ′=6.
′=6.
于是有M′(-8,6).因为M′点在![]() 上,所以3
上,所以3![]() (-8)+6+
(-8)+6+![]() =0,∴
=0,∴![]() =18.
=18.
故直线![]() 的方程为3
的方程为3![]() +
+![]() +18=0 .
+18=0 .

练习册系列答案
相关题目
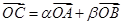 ,其中
,其中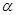
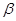 ∈R且
∈R且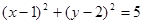 B.3x+2y-11=0 C.2x-y=0 D.x+2y=5
B.3x+2y-11=0 C.2x-y=0 D.x+2y=5