题目内容
已知集合
，
，则
（ ）
A． | B． | C． | D． |
C
解析试题分析：解不等式：
，得
，由并集的概念，可得
.
考点：1、一元二次不等式；2、集合的并集.
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
设
是集合
到对应的集合
的映射，若
，则
等于 （ ）
A． | B． | C． | D． |
设集合
，则
等于（ ）
A． | B． | C． | D． |
若集合
则
中元素个数为 （ ）
| A．0个 | B．1个 | C．2个 | D．3个 |
设集合
，
，若
，则
（ ）
A． | B． | C． | D． |
设全集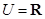
，
，
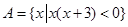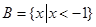，则图中阴影部分表示的集合为（ ）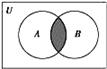
A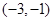． | B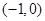． | C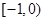． | D． |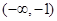
设全集
，则
( )
A． | B． | C． | D． |
若集合
，
，则
所含的元素个数为（ ）
| A．O | B．1 | C．2 | D．3 |
集合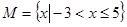
，
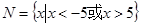，则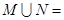
（ ）
A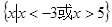． | B． |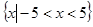
C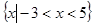． | D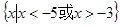． |