题目内容
在△ABC中，三内角A，B，C的大小为等差数列，求sinA+sinC的取值范围．
解：∵三内角A，B，C的大小为等差数列
∴A+B+C=π，A+C=2B，可得3B=π，即B=
∴A+C=
∴sinA+sinC=sinA+sin（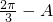
）=
sinA+
cosA=
sin（A+
）
∵0＜A＜
∴＜A+＜
∴
＜sin（A+）≤1
∴sinA+sinC的取值范围是（，]
分析：由题意，可先由三内角A，B，C的大小为等差数列解出B=，从而得出A+C=，再利用和角公式将其变为sin（A+），再由0＜A＜解出其取值范围即可．
点评：本题考查等差数列的性质及三角形的恒等变换公式，解题的关键是熟练利用等差数列的性质建立方程求出角的范围，再由和角公式差角公式化简求值，本题考查了转化的思想及利用公式进行变形计算的能力．
∴A+B+C=π，A+C=2B，可得3B=π，即B=
∴A+C=
∴sinA+sinC=sinA+sin（
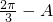）=sinA+cosA=sin（A+）∵0＜A＜
∴
＜A+＜∴
＜sin（A+）≤1∴sinA+sinC的取值范围是（
，]分析：由题意，可先由三内角A，B，C的大小为等差数列解出B=
，从而得出A+C=，再利用和角公式将其变为sin（A+），再由0＜A＜解出其取值范围即可．点评：本题考查等差数列的性质及三角形的恒等变换公式，解题的关键是熟练利用等差数列的性质建立方程求出角的范围，再由和角公式差角公式化简求值，本题考查了转化的思想及利用公式进行变形计算的能力．
练习册系列答案
相关题目