题目内容
下列五个命题:①方程y=kx+2可表示经过点(0,2)的所有直线;
②经过点(x,y)且与直线l:Ax+By+C=0(A,B≠0)平行的直线方程为:A(x-x)+B(y-y)=0;
③在△ABC中,已知a=
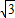 ,A=60°,则
,A=60°,则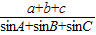 =2;
=2;④函数f(x)=
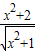 的最小值为2;
的最小值为2;⑤lgx+
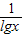 ≥2
≥2 其中真命题是 (把你认为正确的命题序号都填上)
【答案】分析:①利用直线过定点的性质可得①正确.②利用直线平行的性质得平行直线的方程.③利用正弦定理的应用判断.④利用基本不等式的性质判断.
⑤利用基本不等式成立的条件判断.
解答:解:①当直线垂直于x轴时,直线的斜率不存在,所以此时无法方程y=kx+2不能表示,所以①错误.
②利用平行系设和直线l:Ax+By+C=0(A,B≠0)平行的直线方程为Ax+By+m=0,因为直线过点(x,y),
所以Ax+By+m=0,即m=-Ax-By,所以Ax+By-Ax-By=0,所以A(x-x)+B(y-y)=0,所以②正确.
③根据正弦定理得 ,R为三角形外接圆的半径,
,R为三角形外接圆的半径,
因为a= ,A=60°,所以
,A=60°,所以 ,所以③正确.
,所以③正确.
④因为f(x)= =
= ,
,
当且进行 ,即x2+1=1,即x=0时取等号,所以④正确.
,即x2+1=1,即x=0时取等号,所以④正确.
⑤当0<x<1时,lgx<0,不满足基本不等式的条件,所以⑤错误.
故答案为:②③④.
点评:本题主要考查各种命题的真假判断,涉及的知识点较多,综合性较强,要求熟练掌握相应的知识.
⑤利用基本不等式成立的条件判断.
解答:解:①当直线垂直于x轴时,直线的斜率不存在,所以此时无法方程y=kx+2不能表示,所以①错误.
②利用平行系设和直线l:Ax+By+C=0(A,B≠0)平行的直线方程为Ax+By+m=0,因为直线过点(x,y),
所以Ax+By+m=0,即m=-Ax-By,所以Ax+By-Ax-By=0,所以A(x-x)+B(y-y)=0,所以②正确.
③根据正弦定理得
 ,R为三角形外接圆的半径,
,R为三角形外接圆的半径,因为a=
 ,A=60°,所以
,A=60°,所以 ,所以③正确.
,所以③正确.④因为f(x)=
 =
= ,
,当且进行
 ,即x2+1=1,即x=0时取等号,所以④正确.
,即x2+1=1,即x=0时取等号,所以④正确.⑤当0<x<1时,lgx<0,不满足基本不等式的条件,所以⑤错误.
故答案为:②③④.
点评:本题主要考查各种命题的真假判断,涉及的知识点较多,综合性较强,要求熟练掌握相应的知识.

练习册系列答案
相关题目
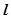 :Ax+By+C=0(A
:Ax+By+C=0(A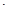 B
B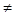 0)垂直的直线方程为: B(x-x0)-A(y-y0)=0;
0)垂直的直线方程为: B(x-x0)-A(y-y0)=0; 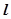 :Ax+By+C=0(A
:Ax+By+C=0(A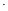 B
B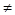 0)垂直的直线方程为: B(x-x0)-A(y-y0)=0;
0)垂直的直线方程为: B(x-x0)-A(y-y0)=0;