题目内容
已知函数![]() 其定义域为[0,2]
其定义域为[0,2]![]() [8,10].
[8,10].
(1)当t=2时,求函数![]() 的值域;
的值域;
(2)当t=2时,求函数![]() 的反函数;
的反函数;
(3)当![]() 在定义域内有反函数时,求t的取值范围.
在定义域内有反函数时,求t的取值范围.
解:(1)当t=2时,![]()
![]() 在[0,2]上为单调减函数,此时
在[0,2]上为单调减函数,此时![]() 的取值范围是[-3,1]
的取值范围是[-3,1]
![]() 在[8,10]上为单调递增函数,此时
在[8,10]上为单调递增函数,此时![]() 的取值范围是[33,61]
的取值范围是[33,61]
![]() 的值域是[-3,1]
的值域是[-3,1]![]() [33,61].
[33,61].
(2)当![]() 时,
时,![]()
得![]()
当![]()
得![]() .
.
互换x, y,得所求反函数为 .
.
(3)由于![]() 所以当
所以当![]() 的定义域内有反函数时,结合图像知有以下情况:
的定义域内有反函数时,结合图像知有以下情况:
(Ⅰ)![]() ;
;
(Ⅱ)当![]()
其中由![]()
则(Ⅱ中)![]()
综上所述,所求t的取值范围是![]() 。
。

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
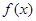 的定义域为R,其导函数
的定义域为R,其导函数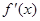 的图像如图所示,则对于任意
的图像如图所示,则对于任意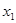 ,
,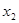
 (
(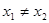 ),下列结论正确的是( )
),下列结论正确的是( )
 ;③
;③ ;
;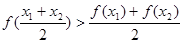 ;⑤
;⑤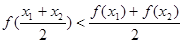 。
。 的定义域为
的定义域为 ,部分函数值如表所示,其导函数的图象如图所示,若正数
,部分函数值如表所示,其导函数的图象如图所示,若正数 ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) 



 B.
B. C.
C. D.
D.
 的定义域为
的定义域为 ,若其值域也为
,若其值域也为 的保值区间是
的保值区间是 ,则
,则 的值为 .
的值为 . 其定义域为[m,n],值域为[3,7],则n+m的最大值是( )
其定义域为[m,n],值域为[3,7],则n+m的最大值是( )