题目内容
(本题满分12分,其中第1小题6分,第2小题6分)
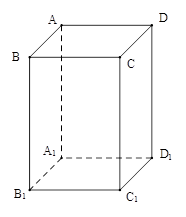
在直三棱柱 中,
中, ,
, ,且异面直线
,且异面直线 与
与 所成的角等于
所成的角等于 ,设
,设
(1)求 的值;
的值;
(2)求直线 到平面
到平面 的距离。
的距离。

在直三棱柱
 中,
中, ,
, ,且异面直线
,且异面直线 与
与 所成的角等于
所成的角等于 ,设
,设
(1)求
 的值;
的值;(2)求直线
 到平面
到平面 的距离。
的距离。
解:(1)

 ,
,
 就是异面直线
就是异面直线 与
与 所成的角,
所成的角,即
 , ………………(2分)
, ………………(2分)又连接
 ,
, ,则
,则

 为等边三角形, ………………(4分)
为等边三角形, ………………(4分)由
 ,
,
 ,
,
 。…………(6分)
。…………(6分)(2)易知
 平面
平面 ,又
,又 是
是 上的任意一点,
上的任意一点,所以点
 到平面
到平面 的距离等于点
的距离等于点 到平面
到平面 的距离.…(8分)
的距离.…(8分)设其为
 ,连接
,连接 ,
,则由三棱锥
 的体积等于三棱锥
的体积等于三棱锥 的体积,求
的体积,求 ,
, 的面积
的面积 ,
, 的面积
的面积 ,………(10分)
,………(10分)又
 平面
平面 ,
,所以
 ,即
,即 到平面
到平面 的距离等于
的距离等于 。…(12分)
。…(12分)略

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
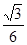

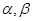 为两个不重合的平面,下列命题中为真命题的是
为两个不重合的平面,下列命题中为真命题的是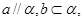 则
则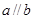
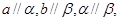 则
则 则
则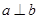
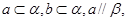 则
则
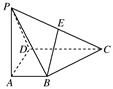
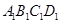 的立柱支撑着一个平行四边形的太阳能电池板(如图),可测得其中三根立柱
的立柱支撑着一个平行四边形的太阳能电池板(如图),可测得其中三根立柱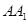 、
、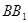 、
、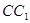 的长度分别为
的长度分别为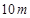 、
、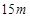 、
、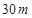 ,则立柱
,则立柱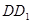 的长度是
的长度是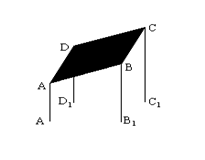

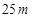
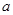 、
、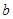 ,
,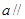 平面
平面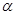 ,则
,则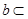 平面
平面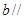 平面
平面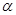 ,b∥
,b∥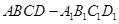 是底面边长为1的正四棱柱,高
是底面边长为1的正四棱柱,高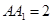 .求:
.求: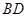 与
与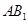 所成的角的大小(结果用反三角函数表示);
所成的角的大小(结果用反三角函数表示);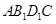 的体积.
的体积.