题目内容
(1)loga2+loga| 1 |
| 2 |
(2)lg20+log10025;
(3)2
| 3 |
| 6 | 12 |
| 3 |
| ||
分析:(1)直接利用对数的运算法则得loga1=0
(2)由对数的换底公式和运算法则log10025=lg5,再由对数的运算法则直接计算即可.
(3)将式子化为分数指数幂形式,利用指数的运算法则求解即可.
(2)由对数的换底公式和运算法则log10025=lg5,再由对数的运算法则直接计算即可.
(3)将式子化为分数指数幂形式,利用指数的运算法则求解即可.
解答:解:(1)loga2+loga
=loga2-loga2=0
(2)lg20+log10025=lg2+1+
=lg2+1+lg5=2
(3)2
×
×
=2×3
×12
×(
)
=21+
-
×3
+
+
=2×3=6
| 1 |
| 2 |
(2)lg20+log10025=lg2+1+
| lg25 |
| 2 |
(3)2
| 3 |
| 6 | 12 |
| 3 |
| ||
| 1 |
| 2 |
| 1 |
| 6 |
| 3 |
| 2 |
| 1 |
| 3 |
| 2 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
点评:本题考查指数、对数的运算法则、对数的换底公式、根式与分数指数幂的互化等,考查运算能力.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目

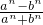 =1(其中n∈N+);
=1(其中n∈N+);
 =1(其中n∈N+);
=1(其中n∈N+);