Question

如图，是由一个圆、一个三角形和一个长方形构成的组合体，现用红、蓝两种颜色为其涂色，每个图形只能涂一种颜色，则三个形状颜色不全相同的概率为________．

Answer 1

分析：首先用分步计数原理分析用两种颜色为3个图形涂色的情况数目，根据题意，分析可得“颜色不全相同”与“颜色全同”为对立事件；易得颜色全同的情况数目，即可得颜色不全相同的情况数目，由古典概型的公式计算可得答案．
解答：根据题意，用红、蓝两种颜色为3个图形涂色，每个图形有2种选择，共2×2×2=8种情况；
其中颜色全部相同的有2种，即全部用红色和蓝色，
则三个形状颜色不全相同的有8-2=6种情况；
故其概率为=；
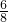故答案为：．
点评：本题考查等可能事件的概率，注意题意中对“颜色不全相同”的理解，即与“颜色全同”为对立事件．