题目内容
(1)抛掷一个骰子,观察出现的点,设事件A为“出现1点”,B为“出现2点”,已知P(A)=P(B)= ,求出现1点或2点的概率;
,求出现1点或2点的概率;
(2)盒子里装有6只红球,4只白球,从中任取3只球,设事件A表示“3只球中有1只红球,2只白球”,事件B表示“3只球中有2只红球,1只白球”,已知P(A)= ,P(B)=
,P(B)= ,求这3只球中既有红球又有白球的概率。
,求这3只球中既有红球又有白球的概率。
 ,求出现1点或2点的概率;
,求出现1点或2点的概率;(2)盒子里装有6只红球,4只白球,从中任取3只球,设事件A表示“3只球中有1只红球,2只白球”,事件B表示“3只球中有2只红球,1只白球”,已知P(A)=
 ,P(B)=
,P(B)= ,求这3只球中既有红球又有白球的概率。
,求这3只球中既有红球又有白球的概率。解:(1)设事件C为“出现1点或2点”,
因为事件A、B是互斥事件,
由C=A∪B可得P(C)=P(A)+P(B)= ,
,
所以出现1点或出现2点的概率是 ;
;
(2)因为A、B是互斥事件,
所以P(A∪B)=P(A)+P(B)= ,
,
所以这3只球中既有红球又有白球的概率是 。
。

练习册系列答案
相关题目
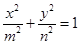
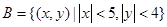 且焦点在X轴的椭圆的概率;
且焦点在X轴的椭圆的概率;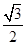 的概率
的概率