题目内容
已知椭圆
+
=1,过左焦点作不垂直与X轴的弦交于椭圆于A.B两点,AB的垂直平分线交X轴于M点,则|MF|:|AB|的值为( )
| x2 |
| 9 |
| y2 |
| 5 |
分析:因为|MF|:|AB|的值为常数,因此采用特殊的直线AB的位置求|MF|:|AB|的值.不妨设直线AB的斜率为1,得直线AB的方程为y=x+2,与椭圆方程消去y得关于x的方程,利用根与系数的关系和弦长公式分别算出|MF|、|AB|的大小,从而得到直线AB的斜率为1时的|MF|:|AB|值,由此即可得到本题的答案.
解答:解:因为|MF|:|AB|的值为常数,与直线AB的方向无关,所以考虑取特殊位置求|MF|:|AB|的值.
取直线的斜率为1,左焦点为F(-2,0)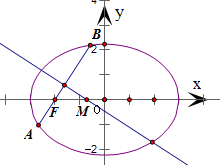
∴直线AB的方程为y=x+2,联立方程组
消去y,整理得14x2+36x-9=0,
设A(x1,y1),B(x2,y2),
由根与系数的关系,得x1+x2=-
,x1x2=-
,
代入直线方程,可得y1+y2=(x1+2)+(x2+2)=
,
∴AB中点坐标为(-
,
),则AB的中垂线方程为y-
=-(x+
),
令y=0,得x=-
,∴点N的坐标(-
,0).
∴|NF|=
=
,|AB|=
=
因此,|MF|:|AB|的值为
:
=
故选:B
取直线的斜率为1,左焦点为F(-2,0)

∴直线AB的方程为y=x+2,联立方程组
|
消去y,整理得14x2+36x-9=0,
设A(x1,y1),B(x2,y2),
由根与系数的关系,得x1+x2=-
| 18 |
| 7 |
| 9 |
| 14 |
代入直线方程,可得y1+y2=(x1+2)+(x2+2)=
| 10 |
| 7 |
∴AB中点坐标为(-
| 9 |
| 7 |
| 5 |
| 7 |
| 5 |
| 7 |
| 9 |
| 7 |
令y=0,得x=-
| 4 |
| 7 |
| 4 |
| 7 |
∴|NF|=
(-
|
| 10 |
| 7 |
2[(-
|
| 30 |
| 7 |
因此,|MF|:|AB|的值为
| 10 |
| 7 |
| 30 |
| 7 |
| 1 |
| 3 |
故选:B
点评:本题给出椭圆焦点弦的垂直平分线,求垂直平分线与x轴交点与焦点距离跟弦长AB的比值,着重考查了椭圆的简单几何性质、直线与椭圆的位置关系等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知椭圆
+y2=1的两个焦点分别为F1,F2,点P在椭圆上且
•
=0,则△PF1F2的面积是( )
| x2 |
| 9 |
| PF1 |
| PF2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
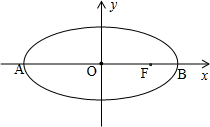 在平面直角坐标系xoy中,如图,已知椭圆
在平面直角坐标系xoy中,如图,已知椭圆