题目内容
正方体A′B′C′D′-ABCD的棱长为a，EF在AB上滑动，且|EF|=b（b＜a），Q点在D′C′上滑动，则四面体A′-EFQ的体积为
- A.与E、F位置有关
- B.与Q位置有关
- C.与E、F、Q位置都有关
- D.与E、F、Q位置均无关，是定值
D
分析：由于|EF|=b，正方体A′B′C′D′-ABCD的棱长为a，可得S△AEF′为定值，点Q到面A′EF的距离为定值a，故得答案．
解答：∵|EF|=b，
正方体A′B′C′D′-ABCD的棱长为a，
∴S△AEF=
ab，
又点Q到面A′EF的距离为定值a，
∴VA′-EFQ=VQ-A′EF．=
•ab•a=
a2b（定值）．
故选D．
点评：本题考查棱锥的体积，关键在于理解与应用轮换顶点的体积公式，属于中档题．
分析：由于|EF|=b，正方体A′B′C′D′-ABCD的棱长为a，可得S△AEF′为定值，点Q到面A′EF的距离为定值a，故得答案．
解答：∵|EF|=b，
正方体A′B′C′D′-ABCD的棱长为a，∴S△AEF=
ab，又点Q到面A′EF的距离为定值a，
∴VA′-EFQ=VQ-A′EF．=
•ab•a=a2b（定值）．故选D．
点评：本题考查棱锥的体积，关键在于理解与应用轮换顶点的体积公式，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
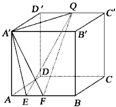正方体A′B′C′D′-ABCD的棱长为a，EF在AB上滑动，且|EF|=b（b＜a），Q点在D′C′上滑动，则四面体A′-EFQ的体积为（ ）
B. 
D. 
