Question

已知直线l的方程为Ax＋By＋C=0，M₁(x₁，y₁)、M₂(x₂，y₂)为直线l异侧的任意两点，M₁、M₃(x₃，y₃)为直线l同侧的任意两点，求证：

(1)Ax₁＋By₁＋C与Ax₂＋By₂＋C异号；

(2)Ax₁＋By₁＋C与Ax₃＋By₃＋C同号.

Answer 1

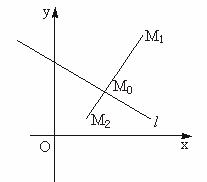
证明:(1)∵M₁、M₂在l异侧，∴l必交线段M₁、M₂于点M₀.

设M₀分M₁M₂所成的比为λ，则分点M₀的坐标为x₀=，y₀=,代入l的方程得

A()＋B()＋C=0.

从而得Ax₁＋By₁＋C＋λ(Ax₂＋By₂＋C)=0.

解出λ，得λ=－.

∵M₀为M₁M₂的内分点，∴λ＞0.

∴Ax₁＋By₁＋C与Ax₂＋By₂＋C异号.

(2)∵M₃、M₁在l同侧，而M₁、M₂在l异侧，

∴M₃、M₂在l异侧.利用(1)得Ax₃＋By₃＋C与Ax₂＋By₂＋C异号,

又∵Ax₁＋By₁＋C与Ax₂＋By₂＋C异号，

∴Ax₁＋By₁＋C与Ax₃＋By₃＋C同号.

点评:此例从理论上证明了二元一次不等式Ax＋By＋C＞0在平面直角坐标系中表示直线Ax＋By＋C=0某一侧所有点组成的平面区域.